PUBLICATIONS

This site contains PDF files of articles that are covered by copyright. You may browse the articles at your convenience in the same spirit as you may read a journal or conference proceedings in a public library. Retrieving, copying, distributing these files, entirely or in parts, may violate copyright protection laws.

RBF Liquids: An Adaptive PIC Solver Using RBF-FD

Rafael Nakanishi Filipe Nascimento Rafael Campos Paulo Pagliosa Afonso Paiva ACM Siggraph Asia 2020 | ACM Transactions on Graphics pdf video webpage link We introduce a novel liquid simulation approach that combines a spatially adaptive pressure projection solver with the Particle-in-Cell (PIC) method. The solver relies on a generalized version of the Finite Difference (FD) method to approximate the pressure field and its gradients in tree-based grid discretizations, possibly non-graded. In our approach, FD stencils are computed by using meshfree interpolations provided by a variant of Radial Basis Function (RBF), known as RBF-Finite-Difference (RBF-FD). This meshfree version of the FD produces differentiation weights on scattered nodes with high-order accuracy. Our method adapts a quadtree/octree dynamically in a narrow-band around the liquid interface, providing an adaptive particle sampling for the PIC advection step. Furthermore, RBF affords an accurate scheme for velocity transfer between the grid and particles, keeping the system’s stability and avoiding numerical dissipation. We also present a data structure that connects the spatial subdivision of a quadtree/octree with the topology of its corresponding dual-graph. Our data structure makes the setup of stencils straightforward, allowing its updating without the need to rebuild it from scratch at each time-step. We show the effectiveness and accuracy of our solver by simulating incompressible inviscid fluids and comparing results with regular PIC-based solvers available in the literature.

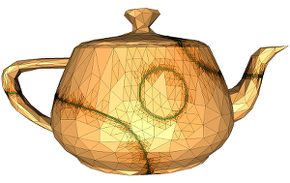
Approximating implicit curves on plane and surface triangulations with affine arithmetic

F.C. Nascimento Afonso Paiva L.H. Figueiredo J. Stolfi Computers & Graphics 40, pp. 36-48, 2014 pdf link We present a spatially and geometrically adaptive method for computing a robust polygonal approximation of an implicit curve defined on a planar region or on a triangulated surface. Our method uses affine arithmetic to identify regions where the curve lies inside a thin strip. Unlike other interval methods, even those based on affine arithmetic, our method works on both rectangular and triangular decompositions and can use any refinement scheme that the decomposition offers.

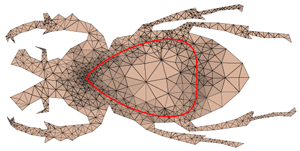
Approximating implicit curves on triangulations with affine arithmetic

Afonso Paiva F.C. Nascimento L.H. Figueiredo J. Stolfi Proceedings of SIBGRAPI 2012, IEEE Press, pp. 94-101, 2012 pdf link We present an adaptive method for computing a robust polygonal approximation of an implicit curve in the plane that uses affine arithmetic to identify regions where the curve lies inside a thin strip. Unlike other interval methods, even those based on affine arithmetic, our method works on triangulations, not only on rectangular quadtrees.