Transformações

Post Original

Sabemos agora como criar objetos, colorir-los e/ou dar-lhes uma aparência detalhada usando texturas, mas eles ainda não são tão interessantes, pois eles são todos objetos estáticos. Poderíamos tentar mover-los ao mudar seus vértices e re-configurar seus buffers a cada quadro, mas isso é complicado e custa bastante poder de processamento. Há muitas maneiras melhores de se transformar um objeto e isso é usando (múltiplos) objetos de matriz ( matrix ). Isso não significa que nós iremo falar sobre Kung Fu e um grande mundo artificial digital.

Matrizes são construções matemáticas muito poderosas que parecem assustadoras no começo, mas uma vez que você se acostuma a elas, vão revelar-se extremamente úteis. Ao discutir matrizes, teremos que mergulhar em um pouco de matemática e para os leitores mais inclinados a matemática vou postar recursos adicionais para leituras posteriores.

No entanto, para compreender plenamente as transformações, primeiro temos que aprofundar um pouco mais em vetores antes de discutir matrizes. O foco deste capítulo é dar-lhe uma base matemática em temas que iremos precisar mais tarde. Se as matérias estiverem difíceis, tente compreendê-las o tanto quanto você puder e volte a este capítulo mais tarde para rever os conceitos sempre que você precisar deles.

Vetores

Em sua definição mais básica, vetores são direções e nada mais. Um vetor tem uma direção e uma magnitude (também conhecida como a sua força ou comprimento). Você pode pensar em vetores como instruções sobre um mapa do tesouro: 'Ande 10 passos para esquerda, agora ande 3 passos na direção norte e 5 passos para direita'; aqui 'esquerda' é a direção e '10 passos' é a magnitude do vetor. As indicações para o mapa do tesouro, portanto, contém 3 vetores. Vetores podem ter qualquer dimensão, mas geralmente trabalhamos com dimensões de 2 a 4. Se um vetor tem 2 dimensões, representa uma direção em um plano (pense em gráficos 2D) e quando ele tem 3 dimensões pode representar qualquer direção em um mundo 3D.

Abaixo, você verá 3 vetores, onde cada vetor é representado com $(x, y)$ como flechas em um gráfico 2D. Como é mais intuitivo para exibir vetores em 2D (ao invés de 3D) você pode pensar dos vetores 2D como vetores 3D com a coordenada $z$ valendo $0$. Já que vetores representam direções, a origem do vetor não muda o seu valor. No gráfico abaixo, podemos ver que os vetores $\bar{v}$ e $\bar{w}$ são iguais mesmo que suas origens sejam diferentes:

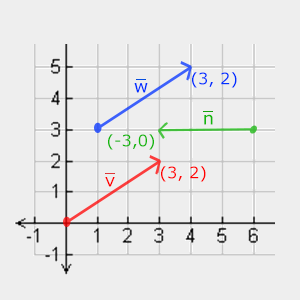
Quando os matemáticos descrevem vetores, geralmente preferem descreve-los através de símbolos com uma barra sobre sua cabeça, como $\bar{v}$. Além disso, em fórmulas eles são geralmente apresentados como se segue:

\[\bar{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}\]

Porque vetores são especificados como direções às vezes é difícil visualizá-los como posições. Se quisermos visualizar vetores como posições podemos imaginar a origem do vetor de direção sendo $(0,0,0)$ e depois apontar para uma certa direção que especifica o ponto, tornando-se um vetor posição (que também pode especificar uma origem diferente e, em seguida, dizer: 'este vetor aponta para esse ponto no espaço a partir desta origem'). O vetor de posição $(3,5)$ apontaria para $(3,5)$ no gráfico com uma origem de $(0,0)$. Usando vetores podemos assim descrever direções e posições no espaço 2D e 3D.

Assim como com números normais também pode definir várias operações em vetores (alguns dos quais você já viu).

Operações Escalares de Vetores

Um escalar é um único número. Ao adicionar / subtrair / multiplicar ou dividir um vetor com um escalar nós simplesmente adicionamos / subtraimos / multiplicamos ou dividimos cada elemento do vetor pelo escalar. Para adição, ficaria assim:

\[\begin {pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + x \rightarrow \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \begin{pmatrix} x \\ x \\ x \end{pmatrix} = \begin{pmatrix} 1 + x \\ 2 + x \\ 3 + x \end{pmatrix}\]

Onde $+$ pode ser $+$, $-$, $\cdot$ ou $\div$ onde $\cdot$ é o operador de multiplicação.

Negação de Vetores

Negar um vetor resulta em um vetor na direção contrária. Um vetor que aponta na direção nordeste apontaria para o sudoeste depois de negação. Para negar um vetor, adicionamos um sinal de menos em cada componente (você também pode representá-lo como uma multiplicação escalar-vetor com um valor escalar $-1$):

\[-\bar{v} = -\begin{pmatrix} v_x \\ v_y \\ v_z \end{pmatrix} = \begin{pmatrix} - v_x \\ - v_y \\ - v_z \end{pmatrix}\]

Adição e Subtração

A adição de dois vetores é definida como a adição por componente ( component-wise ), isto é, cada componente de um vetor é adicionada a mesma componente do outro vetor da seguinte forma:

\[\bar{v} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \bar{k} = \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix} \rightarrow \bar{v} + \bar{k} = \begin{pmatrix} 1 + 4 \\ 2 + 5 \\ 3 + 6 \end{pmatrix} = \begin{pmatrix} 5 \\ 7 \\ 9 \end{pmatrix}\]

Visualmente, para os vetores v = (4,2) e k = (1,2), em que o segundo vetor é adicionado em cima da extremidade do primeiro vetor para encontrar o ponto final do vetor resultante (método head-to-tail):

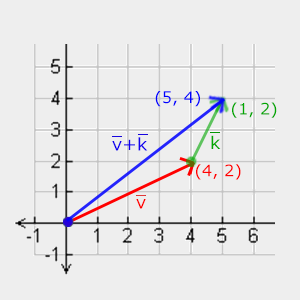
Assim como adição e subtração normais, a subtração de vetores é o mesmo que a adição com o segundo vetor negado:

\[\bar{v} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \bar{k} = \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix} \rightarrow \bar{v} + - \bar{k} = \begin{pmatrix} 1 + (-4) \\ 2 + (-5) \\ 3 + (-6) \end{pmatrix} = \begin{pmatrix} - 3 \\ - 3 \\ -3 \end{pmatrix}\]

Subtraindo-se dois vetores um do outro resulta num vetor que é a diferença das posições que apontam ambos os vetores. Isso se prova útil em certos casos em que precisamos recuperar um vetor que é a diferença entre dois pontos.

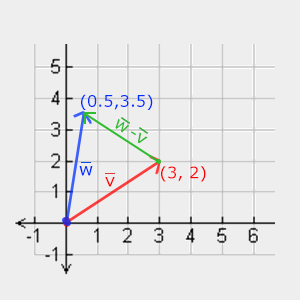
Comprimento (Length)

Para recuperar o comprimento/magnitude de um vetor usamos o teorema de Pitágoras que você pode se lembrar de suas aulas de matemática. Um vetor forma um triângulo quando visualizamos sua componentes individuais x e y como dois lados de um triângulo:

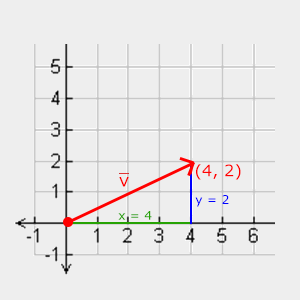
Já o comprimento dos dois lados (x, y) são conhecidos e queremos saber o comprimento do lado inclinado $\bar{v}$, podemos calcula-lo usando o teorema de Pitágoras:

\[|| \bar{v}|| = \sqrt{ x^2 + y^2}\]

Onde $||\bar{v}||$ é denotado como o comprimento do vetor $\bar{v}$. Isto é facilmente estendido para 3D adicionando $z^2$ para a equação.

Neste caso, o comprimento do vetor (4, 2) é igual a:

\[||\bar{v}|| = \sqrt{ 4^2 + 2^2} = \sqrt{16 + 4} = \sqrt{20} = 4.47\]

Que é 4.47.

Há também um tipo especial de vetor que nós chamamos um vetor unitário ( unit vetor ). Um vetor unitário tem uma propriedade extra que é que seu comprimento é exatamente 1. Nós podemos calcular um vetor unitário $\hat{n}$ a partir de qualquer vetor, dividindo cada um dos componentes do vetor por seu comprimento:

\[\hat{n} = \frac{\bar{v}}{|| \bar{v} ||}\]

Chamamos isso de normalizar um vetor. Vetores unitários são exibidos com um chapéu sobre sua cabeça e geralmente são mais fáceis de trabalhar, especialmente quando nos preocupamos apenas com suas direções (a direção não muda se mudarmos o comprimento de um vetor).

Multiplicação Vetor-Vetor

A multiplicação de dois vetores se trata de um caso um pouco estranho. A multiplicação normal não está realmente definida em vetores, uma vez que não tem sentido visual, mas temos dois casos específicos dos quais que poderíamos escolher ao multiplicar: um é o produto escalar ( dot product ) denotado como $\bar{v} \cdot \bar {k}$ e o outro é o produto vetorial ( cross product ) denotado como $\bar{v} \times \bar{k}$.

Produto Escalar

O produto escalar de dois vetores é igual ao produto escalar dos seus comprimentos vezes o coseno do ângulo entre eles. Se isso soa confuso, dê uma olhada na sua fórmula:

\[\bar{v} \cdot \bar{k} = || \bar{v} || \cdot || \bar{k} || \cdot \cos \theta\]

Onde o ângulo entre eles é representado por theta ($\theta$). Por que isso é interessante? Bem, imagine se $\bar{v}$ e $\bar{k}$ são vetores unitários. Isso efetivamente reduz a fórmula para:

\[\hat{v} \cdot \hat{k} = 1 \cdot 1 \cdot \cos \theta = \cos \theta\]

Agora, o produto escalar só define o ângulo entre os dois vetores. Você pode se lembrar que o coseno ou a função cos se torna 0 quando o ângulo é de 90 graus ou 1 quando o ângulo é 0. Isso nos permite facilmente testar se os dois vetores são ortogonais ou paralelos entre si usando o produto escalar (ortogonais significa que os vetores formam um ângulo reto um com o outro). No caso de você querer saber mais sobre as funções sin e cos sugiro os seguintes vídeos da Khan Academy sobre trigonometria básica.

Então, como podemos calcular o produto escalar? O produto escalar é a multiplicação por componente onde adicionamos os resultados. Com dois vetores unitários (você pode verificar que ambos os seus comprimentos são exatamente 1):

\[\begin{pmatrix} 0.6 \\ - 0.8 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} = 0.6 * 0) + (-0.8 * 1) + (0 * 0) = -0.8\]

Para calcular o ângulo entre estes dois vetores unitários, usamos o inverso da função coseno $\cos^{-1}$ e isto resulta em 143.1 graus. Nós agora efetivamente calculamos o ângulo entre esses dois vetores. O produto escalar será muito útil para fazer cálculos de iluminação mais tarde.

Produto Vetorial

O produto vetorial é apenas definido no espaço 3D e leva dois vetores não-paralelos como entrada e produz um terceiro vetor que é ortogonal a ambos os vetores de entrada. Se ambos os vetores de entrada são ortogonais entre si, o produto vetorial resultaria em 3 vetores ortogonais; isso vai ser útil nos próximos capítulos. A imagem seguinte mostra como isso parece no espaço 3D:

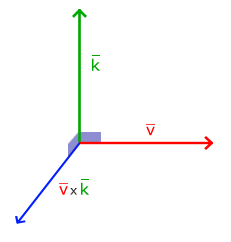
Ao contrário das outras operações, o produto vetorial não é muito intuitivo sem aprofundarmos na álgebra linear, por isso é melhor apenas memorizar a fórmula e você vai ficar bem (ou não, você provavelmente vai ficar bem também). Abaixo, você verá o produto vetorial entre dois vetores ortogonais A e B:

\[\begin{pmatrix} A_{x} \\ A_y \\ A_ {z} \end{pmatrix} \times \begin{pmatrix} B_{x} \\ B_y \\ B_{z} \end{pmatrix} = \begin{pmatrix} A_{y} \cdot B_{z} - A_{z} \cdot B_{y} \\ A_{z} \cdot B_{x} - A_{x} \cdot B_{z} \\ A_{x} \cdot B_{y} - A_{y} \cdot B_{x} \end{pmatrix}\]

Como você pode ver, ele realmente não parece fazer sentido. No entanto, se você apenas seguir estes passos você obterá um outro vetor que é perpendicular aos seus vetores de entrada.

Matrizes

Agora que nós discutimos quase tudo o que há de vetores é hora de entrar na Matrix! Uma matriz é um array retangular de números, símbolos e/ou expressões matemáticas. Cada item individual numa matriz é chamado um elemento da matriz. Um exemplo de uma matriz de 2x3 é mostrado abaixo:

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}\]

As matrizes são indexadas por (i, j), onde i é a linha e j é a coluna, por isso a matriz acima é chamada uma matriz de 2x3 (3 colunas e 2 linhas, também conhecida como as dimensões da matriz). Este é o oposto do que você está acostumado ao indexar gráficos 2D como (x, y). Para recuperar o valor 4 teríamos posicioná-lo como (2,1) (segunda linha, primeira coluna).

Matrizes são basicamente nada mais do que isso, apenas arrays retangulares de expressões matemáticas. Elas têm um conjunto de propriedades matemáticas muito bom e, assim como vetores podemos definir várias operações sobre matrizes como: adição, subtração e multiplicação.

Adição e Subtração

A adição e subtração entre duas matrizes são feitas em uma base por-elemento. Assim, as mesmas regras gerais com os números normais de que estamos familiarizados aplicam-se, mas feito sobre os elementos de ambas as matrizes com o mesmo índice. Isto significa que a adição e subtração só é definida para matrizes com as mesmas dimensões. Uma matriz 3x2 e uma matriz de 2x3 (ou uma matriz 3x3 e uma matriz 4x4) não podem ser adicionadas ou subtraídas. Vamos ver como a adição de matriz funciona em duas matrizes 2x2:

\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix}\]

As mesmas regras se aplicam para a subtração de matriz:

\[\begin{bmatrix} 4 & 2 \\ 1 & 6 \end{bmatrix} - \begin{bmatrix} 2 & 4 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 4 - 2 & 2 - 4 \\ 1 - 0 & 6 - 1 \end{bmatrix} = \begin{bmatrix} 2 & -2 \\ 1 & 5 \end{bmatrix}\]

Produtos Matriz-Escalar

Um produto matriz-escalar multiplica cada elemento da matriz pelo escalar. O exemplo a seguir ilustra a multiplicação:

\[ 2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 2 \cdot 1 & 2 \cdot 2 \\ 2 \cdot 3 & 2 \cdot 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 8 & 6 \end{bmatrix} \]

Agora também faz sentido a respeito de porque esses números individuais são chamados de escalares. Um escalar basicamente escala todos os elementos da matriz pelo seu valor. No exemplo anterior, todos os elementos foram escalados por dois.

Até aí tudo bem, todos os nossos casos não foram realmente muito complicados. Isto é, até começarmos com a multiplicação matriz-matriz.

Multiplicação Matriz-Matriz

Multiplicar as matrizes não é necessariamente complexo, mas bastante difícil de se sentir confortável com. A multiplicação de matrizes significa, basicamente, seguir um conjunto de regras pré-definidas. Existem algumas restrições, porém:

1. Você só pode multiplicar duas matrizes se o número de colunas na matriz do lado esquerdo é igual ao número de linhas na matriz do lado direito.

2. A multiplicação de matrizes não é comutativa , que é $A \cdot B \neq B \cdot A$.

Vamos começar com um exemplo de uma multiplicação de 2 matrizes 2x2:

\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \cdot \begin{bmatrix} \ 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 1 \cdot 5 + 2 \cdot 7 & 1 \cdot 6 + 2 \cdot 8 \\ 3 \cdot 5 + 4 \cdot 7 & 3 \cdot 6 + 4 \cdot 8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}\]

Agora você provavelmente está tentando descobrir o que diabos aconteceu? A multiplicação de matrizes é uma combinação de multiplicação e adição normais utilizando as linhas da matriz esquerda com colunas da matriz direita. Vamos tentar discutir isso com a seguinte imagem:

Em primeiro lugar, tomamos a linha superior da matriz esquerda e depois tomamos uma coluna da matriz direita. A linha e coluna que escolhemos decide que valor da matriz 2x2 vamos calcular. Se tomarmos a primeira linha da matriz esquerda o valor resultante vai acabar na primeira linha da matriz resultante, então nós escolhemos uma coluna e se é a primeira coluna o valor do resultado vai acabar na primeira coluna da matriz resultante. Este é exatamente o caso do caminho vermelho. Para calcular o resultado inferior direito tomamos a linha inferior da primeira matriz e da coluna mais à direita da segunda matriz.

Para calcular o valor resultante multiplicamos os primeiros elementos da linha e da coluna, utilizando multiplicação normal, fazemos o mesmo para os segundos elementos, terceiros, quartos, etc. Os resultados das multiplicações individuais são então somados e temos o nosso resultado. Agora, também faz sentido que um dos requisitos é que o tamanho das colunas de matriz esquerda e o número de linhas da matriz direita sejam iguais, caso contrário, não podemos terminar as operações!

O resultado é, em seguida, uma matriz que tem dimensões de (n, m), onde n é igual ao número de linhas da matriz do lado esquerdo e m é igual ao número de colunas da matriz do lado direito.

Não se preocupe se você tem dificuldades imaginando as multiplicações dentro de sua cabeça. Apenas continue tentando fazer os cálculos à mão e retorne a esta página sempre que você tiver dificuldades. Com o tempo, a multiplicação de matrizes torna-se natural para você.

Vamos acabar com a discussão de multiplicação de matriz-matriz com um exemplo maior. Tente visualizar o padrão usando as cores. Como um exercício útil, veja se você consegue chegar sozinho(a) a mesma resposta (uma vez que você tentar fazer uma multiplicação de matrizes à mão você vai rapidamente obter a compreensão delas).

\[\begin{bmatrix} 4 & 2 & 0 \\ 0 & 8 & 1 \\ 0 & 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 4 & 2 & 1 \\ 2 & 0 & 4 \\ 9 & 4 & 2 \end{bmatrix} = \begin{bmatrix} 4 \cdot 4 + 2 \cdot 2 + 0 \cdot 9 & 4 \cdot 2 + 2 \cdot 0 + 0 \cdot 4 & 4 \cdot 1 + 2 \cdot 4 + 0 \cdot 2 \\ 0 \cdot 4 + 8 \cdot 2 + 1 \cdot 9 & 0 \cdot 2 + 8 \cdot 0 + 1 \cdot 4 & 0 \cdot 1 + 8 \cdot 4 + 1 \cdot 2 \\ 0 \cdot 4 + 1 \cdot 2 + 0 \cdot 9 & 0 \cdot 2 + 1 \cdot 0 + 0 \cdot 4 & 0 \cdot 1 + 1 \cdot 4 + 0 \cdot 2 \end{bmatrix} \\ = \begin{bmatrix} 20 & 8 & 12 \\ 25 & 4 & 34 \\ 2 & 0 & 4 \end{bmatrix}\]

Como você pode ver, a multiplicação de matrizes é um processo bastante complicado e muito propenso a erros (é por isso que normalmente deixamos para os computadores fazerem) e isso fica problemático bem rápido quando as matrizes se tornam maiores. Se você ainda está sedento por mais e você está curioso sobre mais algumas das propriedades matemáticas de matrizes eu sugiro fortemente que você dê uma olhada nestes vídeos da Khan Academy a cerca de matrizes.

De qualquer forma, agora que sabemos como multiplicar matrizes, podemos começar com as coisas boas agora.

Multiplicação Matriz-Vetor

Até agora nós tivemos nossa boa parcela de vetores. Nós os utilizamos para representar posições, cores e até mesmo coordenadas de textura. Vamos adentrar mais um pouco na toca do coelho e dizer que um vetor é basicamente uma matriz Nx1, onde N é o número de componentes do vetor (também conhecido como um vetor n-dimensional ). Se você pensar sobre isso, faz muito sentido. Os vetores são como matrizes, um array de números, mas com apenas uma coluna. Então, como esta nova informação nos ajuda? Bem, se temos uma matriz MxN podemos multiplicar esta matriz com o nosso vetor Nx1, já que o número de colunas da matriz é igual ao número de linhas do vetor, assim, a multiplicação de matrizes é definida.

Mas porque é que nós nos importamos se podemos multiplicar matrizes com um vetor? Bem, acontece que há muitas transformações 2D / 3D interessantes que podemos colocar dentro de uma matriz, e multiplicando a matriz com um vetor, em seguida, transformamos esse vetor. No caso de você ainda estar um pouco confuso, vamos começar com alguns exemplos e em breve você vai ver o que queremos dizer.

Matriz Identidade

Em OpenGL normalmente trabalhamos com matrizes de transformação 4x4 por várias razões e uma delas é que a maioria dos vetores são de tamanho 4. A matriz de transformação mais simples que podemos pensar é a matriz identidade. A matriz de identidade é uma matriz NxN com apenas 0s exceto na sua diagonal. Como você verá, esta transformação de matriz deixa um vetor completamente ileso:

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \\ 3 \end{bmatrix} = \begin{bmatrix} 1 \cdot 1 \\ 1 \cdot 2 \\ 1 \cdot 3 \\ 1 \cdot 4 \end{bmatrix} = \begin{bmatrix} 1 \\ 2\\3 \\ 4 \end{bmatrix}\]

O vetor está completamente intacto. Isto torna-se óbvio a partir das regras de multiplicação: o primeiro elemento é resultado de cada elemento individual da primeira linha da matriz multiplicado com cada elemento do vetor. Uma vez que cada um dos elementos da linha são 0, exceto a primeira, obtemos: $ 1 \cdot 1 + 0 \cdot 2 + 0 \cdot 3 + 0 \cdot 4 = 1$ e o mesmo se aplica para os outros 3 elementos do vetor.

Escala

Quando escalamos um vetor estamos aumentando o comprimento da flecha pela quantidade que gostaríamos de escalar, mantendo sua direção. Uma vez que estamos trabalhando em 2 ou 3 dimensões, podemos definir a escala por um vetor de 2 ou 3 variáveis ​​de escalonamento, cada uma dimensionando um eixo (x, y ou z).

Vamos tentar escalar o vetor $\bar{v} = (3,2)$. Vamos escalar o vetor ao longo do eixo x por 0.5, tornando-se, assim, duas vezes mais estreito; e vamos escalar o vetor por 2 ao longo do eixo y, tornando-se duas vezes mais alto. Vamos ver o que acontece se dimensionarmos o vetor por (0.5,2) como $\bar{s}$:

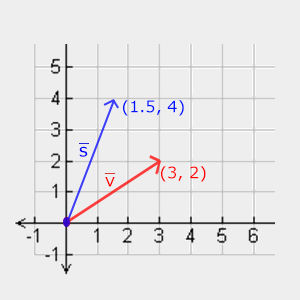
Tenha em mente que OpenGL normalmente opera no espaço 3D, então para este caso 2D poderíamos definir a escala do eixo z como 1, deixando-a ilesa. A operação de escala que acabamos de realizar se trata de uma escala não uniforme , porque o fator de escala não é o mesmo para cada eixo. Se o escalar fosse igual em todos os eixos seria chamada de uma escala uniforme .

Vamos começar a construir uma matriz de transformação que faz a escala. Vimos a partir da matriz de identidade que cada um dos elementos da diagonal foram multiplicados com o seu elemento de vetor correspondente. E se mudássemos os 1s na matriz de identidade para 3s? Nesse caso, estaríamos multiplicando cada um dos elementos do vetor por um valor de 3 e assim, efetivamente uniformemente escalaríamos o vetor por 3. Se representarmos as variáveis ​​de escala como $(S_1, S_2, S_3)$, podemos definir uma matriz de dimensionamento em qualquer vetor $(x, y, z)$ como:

\[\begin{bmatrix} S_1 & 0 & 0 & 0 \\ 0 & S_2 & 0 & 0 \\ 0 & 0 & S_3 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} S_1 \cdot x \\ S_2 \cdot y \\ S_3 \cdot z \\ 1 \end{pmatrix}\]

Note que mantemos o quarto valor de escala como 1. O componente w é usado para outros fins, como veremos mais tarde.

Translação

A translação é o processo de adição de um outro vetor em cima do vetor original para obter um novo vetor com uma posição diferente, movendo-se assim o vetor baseado em um vetor de translação. Nós já falamos sobre adição de vetores de modo que isto não deve ser muito novo.

Assim como a matriz de escala existem vários locais em uma matriz de 4 por 4, que podemos usar para executar determinadas operações, e para a translação esses são os 3 principais valores da quarta coluna. Se nós representasse-mos o vetor de translação como $(T_x, T_y, T_z)$ poderíamos definir a matriz de translação por:

\[\begin{bmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = \begin{pmatrix} x + T_x \\ y + T_y \\ z + T_z \\ 1 \end{pmatrix}\]

Isso funciona porque todos os valores de translação são multiplicados pela linha w do vetor e acrescentados aos valores originais do vetor (lembre-se das regras de multiplicação de matrizes). Isto não teria sido possível com uma matriz 3-por-3.

Com uma matriz de translação podemos mover objetos em qualquer uma das 3 direções dos eixos (x, y, z), tornando-se uma matriz de transformação muito útil para a nossa caixa de ferramentas de transformação.

Rotação

As últimas transformações eram relativamente fáceis de entender e visualizar nos espaços 2D ou 3D, mas rotações são um pouco mais complicadas. Se você quer saber exatamente como essas matrizes são construídas eu recomendo que você assista os itens de rotação dos vídeos de álgebra linear da Khan Academy.

Primeiro vamos definir o que uma rotação de um vetor é realmente. Uma rotação em 2D ou 3D é representada com um ângulo . Um ângulo poderia estar em graus ou radianos, onde um círculo completo tem 360 graus ou 2 PI radianos. Eu prefiro explicar rotações usando graus já que geralmente mais acostumados a eles.

A rotação pela metade de um círculo nos gira 360/2 = 180 graus e a rotação de 1/5 para a direita significa que giramos 360/5 = 72 graus para a direita. Isto é demonstrado por uma vetor 2D onde $\bar{v}$ é rotacionado de 72 graus para a direita, ou no sentido horário, a partir de $\bar{k}$:

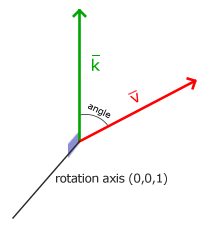
Rotações em 3D são especificados com um ângulo e de um eixo de rotação . O ângulo específico, vai rodar o objecto ao longo do eixo de rotação dado. Tente visualizar girando sua cabeça um certo grau enquanto continuamente olhando para na direção de um eixo de rotação único. Ao rodar os vetores 2D num mundo 3D por exemplo, definimos o eixo de rotação para o eixo z (tente visualizar).

Usando a trigonometria, é possível transformar vetores para novos vetores girados a um ângulo. Isso geralmente é feito através de uma combinação inteligente das funções seno e cosseno (comumente abreviados para sin e cos). A discussão de como as matrizes de rotação são geradas está fora do escopo deste capítulo.

Uma matriz de rotação é definida para cada eixo unitário no espaço 3D, onde o ângulo é representado como o símbolo teta $\theta$.

Rotação em torno do eixo-X:

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ \cos\theta \cdot y - \sin\theta \cdot z \\ \sin\theta \cdot y + \cos\theta \cdot z \\ 1 \end{pmatrix}\]

Rotação em torno do eixo Y:

\[\begin{bmatrix} \cos\theta & 0 & \sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ - \sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \cos\theta \cdot x + \sin\theta \cdot z \\ y \\ - \sin\theta \cdot x + \cos \theta \cdot z \\ 1 \end{pmatrix}\]

Rotação em torno do eixo Z:

\[\begin{bmatrix} \cos\theta & - \sin\theta & 0 & 0 \\ \sin\theta & \cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \cos\theta \cdot x - \sin\theta \cdot y \\ \sin\theta \cdot x + \cos\theta \cdot y \\ z \\ 1 \end{pmatrix}\]

Usando as matrizes de rotação podemos transformar os nossos vetores posição em torno de um dos três eixos unitários. Para girar em torno de um eixo 3D arbitrário podemos combinar todos 3, em primeiro lugar girar em torno do eixo X, em seguida, Y e Z, por exemplo. No entanto, isto rapidamente introduz um problema chamado Gimbal Lock . Não vamos discutir os detalhes, mas uma solução melhor para girar em torno de um eixo unitário arbitrário por exemplo (0.662,0.2,0.722) (note que este é um vetor unitário) de imediato, em vez de combinar as matrizes de rotação. Tal matriz existe e é dada abaixo com $(R_x,R_y,R_z)$ como o eixo de rotação arbitrária:

\[\begin{bmatrix} \cos \theta + R_x^2 (1 - \cos\theta) & {R_x} {R_y} (1 - \cos \theta) - {R_z} \sin \theta & {R_x} {R_z} (1 - \cos \theta) + { R_y} \sin \theta & 0 \\ {R_y} {R_x} (1 - \cos \theta) + {R_z} \sin \theta & \cos \theta + {R_y} ^ 2 (1 - \cos \theta) & {R_y} {R_z} (1 - \cos \theta) - R_x \sin \theta & 0 \\ {R_z} {R_x} (1 - \cos \theta) - {R_y} \sin \theta & {R_z} {R_y} (1 - \cos \theta) + {R_x} \sin \theta & \cos \theta + { R_z} ^ 2 (1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

Uma discussão matemática sobre gerar tal matriz está fora do âmbito deste capítulo. Tenha em mente que mesmo essa matriz não impede completamente Gimbal locks (embora fique muito mais difícil). Para evitar que verdadeiramente Gimbal locks temos que representar rotações usando quaternions , que não só são mais seguros, mas também computacionalmente mais amigáveis. No entanto, uma discussão sobre quaternions está fora do escopo deste capítulo.

Combinando Matrizes

O verdadeiro poder de usar matrizes para transformações é que podemos combinar várias transformações em uma única matriz, graças à multiplicação de matriz-matriz. Vamos ver se podemos gerar uma matriz de transformação que combina várias transformações. Digamos que temos um vetor (x, y, z) e que queremos dimensioná-lo por 2 e, em seguida, movê-lo por (1,2,3). Precisamos de uma matriz de translação e uma matriz de escala para nossos passos. A matriz de transformação resultante seria semelhante a:

\[Trans. Escala = \begin{bmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 3 \\ 0 & 0 & 0 & 1 \end{bmatrix}. \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 0 & 0 & 1 \\ 0 & 2 & 0 & 2 \\ 0 & 0 & 2 & 3 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

Note que primeiro fazemos uma translação e, em seguida, uma transformação de escala ao multiplicar matrizes. A multiplicação de matrizes não é comutativa, o que significa que sua ordem é importante. Ao multiplicar matrizes, a matriz mais à direita é multiplicada primeiro com o vetor de modo que você deve ler as multiplicações da direita para a esquerda. É aconselhável primeiro fazer escalas, em seguida, rotações e, por último translações quando combinando matrizes, caso contrário elas podem (negativamente) afetar umas as outras. Por exemplo, se você primeiro fazer uma translação e, em seguida, escala, o vetor de translação também será escalado!

Executando a matriz de transformação final sobre nosso vetor resulta em:

\[\begin{bmatrix} 2 & 0 & 0 & 1 \\ 0 & 2 & 0 & 2 \\ 0 & 0 & 2 & 3 \\ 0 & 0 & 0 & 1 \end{bmatrix}. \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} 2x + 1 \\ 2y + 2 \\ + 2z 3 \\ 1 \end{bmatrix}\]

Ótimo! O vetor é primeiramente escalonado por dois e, em seguida, transladado por (1,2,3).

Na Prática

Agora que nós explicamos toda a teoria por trás de transformações, é hora de ver como nós podemos realmente usar esse conhecimento para nossa vantagem. A OpenGL não tem qualquer forma de conhecimento de matriz ou vetor embutidos, por isso temos de definir nossas próprias classes de matemática e funções. Neste livro, prefiro abstrair de todos os pequenos detalhes matemáticos e simplesmente usar bibliotecas pré-fabricadas de matemática. Felizmente, há uma biblioteca matemática adaptada para OpenGL fácil de usar e chamada GLM.

GLM

GLM significa OpenGL Mathematics e é uma biblioteca de apenas cabeçalhos, o que significa que só temos de incluir os arquivos de cabeçalho adequados e estamos prontos; sem vinculação e compilação necessárias. A GLM pode ser baixada de seu site. Copie o diretório raiz dos arquivos de cabeçalho em sua pasta include e vamos brincar.

A maioria das funcionalidades da GLM que precisamos podem ser encontradas em 3 arquivos cabeçalhos que vamos incluir a seguir:

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

Vamos ver se podemos colocar nosso conhecimento de transformações em prática, transladando um vetor de (1,0,0) por (1,1,0) (note que o definimos como glm::vec4 com sua coordenada homogênea definida para 1.0:

glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;

Nós primeiro definimos um vetor chamado vec usando a classe de vetor da GLM. Em seguida, definimos uma mat4 e a inicializamos explicitamente com uma matriz identidade ao definir a diagonal da matriz com 1.0; se não inicializar com a matriz identidade a matriz seria uma matriz nula (todos os elementos 0) e todas as operações da matriz subseqüentes iriam acabar em uma matriz nula também.

O próximo passo é para criar uma matriz de transformação, passando a matriz de identidade para a função a glm::translate, juntamente com um vetor de translação (a matriz é então multiplicada por uma matriz de translação e a matriz resultante é devolvida).

Depois multiplicamos nosso vetor pela matriz de transformação. Se ainda nos lembramos como a matriz de translação funciona, então o vetor resultante deve ser **(1 + 1,0 + 1,0 + 0)** que é **(2,1,0)**. Este trecho de código gera **210** de modo a matriz de translação fez o seu trabalho.

Vamos fazer algo mais interessante e escalar e girar o objeto do capítulo anterior:

glm::mat4 trans = glm::mat4(1.0f);
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));  

Em primeiro lugar, dimensionamos o objeto de 0.5 em cada um dos eixos e em seguida rodamos o objeto 90 graus em torno do eixo Z. A GLM espera seus ângulos em radianos, então convertemos os graus em radianos usando glm::radianos. Note que o retângulo texturizado está no plano XY por isso queremos girar em torno do eixo Z. Tenha em mente que o eixo que giramos em torno deve ser um vetor de unidade, por isso tenha certeza de normalizar o vetor primeiro se você não está girando em torno do eixo X, Y ou Z. Como passamos a matriz para cada uma das funções da GLM, a GLM automaticamente multiplica as matrizes em conjunto, resultando em uma matriz de transformação que combina todas as transformações.

A próxima grande questão é: como é que vamos acessar a matriz de transformação dos shaders? Nós brevemente mencionamos antes que a GLSL também tem um tipo mat4. Então, vamos adaptar o shader de vértice para aceitar uma variável uniforme mat4 e multiplicar o vetor posição pelo uniforme de matriz:

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;

out vec2 TexCoord;
  
uniform mat4 transform;

void main()
{
    gl_Position = transform * vec4(aPos, 1.0f);
    TexCoord = vec2(aTexCoord.x, aTexCoord.y);
} 

Adicionamos o uniforme e multiplicamos o vetor de posição com a matriz de transformação antes de passá-lo para gl_Position . O nosso objeto deve agora ser duas vezes mais pequeno e rotationado 90 graus (inclinado para a esquerda). No entanto, ainda precisamos passar a matriz de transformação para o shader:

unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));

Em primeiro lugar, consultamos a localização da variável uniforme e, em seguida, enviamos os dados da matriz para os shaders utilizando glUniform com Matrix4fv como posfixo. O primeiro argumento deve ser familiar agora, que é a localização do uniforme. O segundo argumento diz a OpenGL quantas matrizes gostaríamos de enviar, que é 1. O terceiro argumento nos pergunta se queremos transpor nossa matriz, que é trocar as colunas e linhas. desenvolvedores OpenGL costumam usar um layout de matriz interna chamada column-major ordering que é o layout da matriz padrão no GLM por isso não há necessidade de transpor as matrizes; podemos mantê-lo em GL_FALSE . O último parâmetro são os dados da matriz, mas GLM armazena os dados de suas matrizes de uma maneira que nem sempre corresponde às expectativas da OpenGL, então primeiro convertemos os dados com a função da GLM value_ptr .

Nós criamos uma matriz de transformação, declaramos um uniforme no shader de vértice e enviamos a matriz para os shaders que transformam nossas coordenadas dos vértices. O resultado deve ser algo como isto:

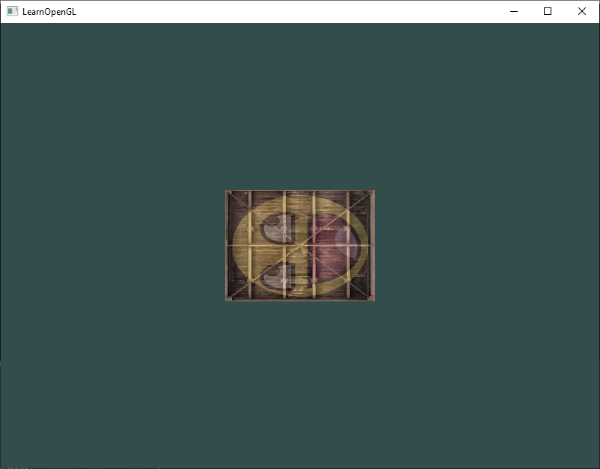
Perfeito! Nosso objeto está realmente inclinado para a esquerda e duas vezes mais pequeno logo a transformação foi bem sucedida. Vamos brincar um pouco mais e ver se podemos rodar o objeto ao longo do tempo, e para se divertir também vamos reposicionar o objeto no lado inferior direito da janela. Para roda-lo ao longo do tempo nós temos que atualizar a matriz de transformação no loop de renderização porque ele precisa ser atualizado a cada quadro. Nós usamos a função do tempo da GLFW para obter um ângulo ao longo do tempo:

glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));

Tenha em mente que no caso anterior, poderíamos declarar a matriz de transformação em qualquer lugar, mas agora temos que criá-la cada iteração para atualizar continuamente a rotação. Isto significa que temos para recriar a matriz de transformação em cada iteração do loop de renderização. Normalmente, na renderização de cenas temos várias matrizes de transformação que são recriadas com novos valores cada quadro.

Aqui podemos rodar o objeto em torno da origem (0,0,0) e uma vez que é rodado, transladamos a sua versão rotacionada para o canto inferior direito da tela. Lembre-se que a ordem de transformação deve ser lida ao contrário: mesmo que no código primeiro translademos e depois giremos, as transformações reais primeiro aplicam uma rotação e depois uma translação. Compreender todas estas combinações de transformações e como se aplicam a objetos é difícil de entender. Experimente e tentar transformações como estas e você vai rapidamente ter uma idéia melhor.

Se você fez as coisas direito, deve obter o seguinte resultado:

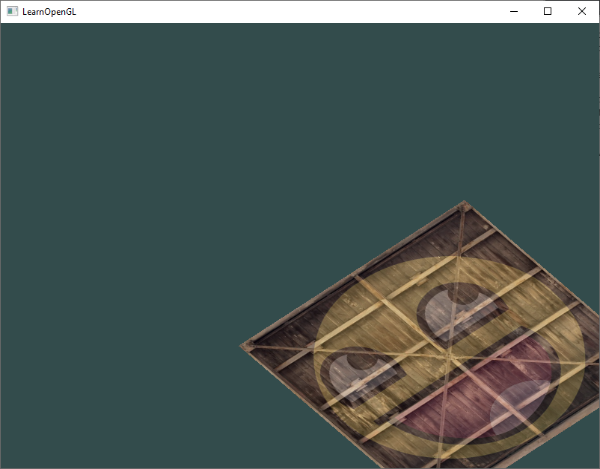
E aí está. Um objeto transladado que é rotacionando com o tempo, tudo feito por uma única matriz de transformação! Agora você pode ver porque matrizes são uma construção tão poderosa na terra dos gráficos. Podemos definir uma quantidade infinita de transformações e combiná-las em uma única matriz que podemos voltar a usar tão frequentemente como gostaríamos. Usando transformações como esta no shader de vértice nos salva o esforço de redefinição dos dados de vértice e nos poupa algum tempo de processamento, bem como, uma vez que não temos que re-enviar os nossos dados o tempo todo (que é bastante lento); tudo o que precisamos fazer é atualizar o uniforme de transformação.

Se você não obter o resultado correto ou se você estiver preso(a) em algum lugar, dê uma olhada no código fonte e a classe shader atualizada.

No próximo capítulo vamos discutir como podemos usar matrizes para definir diferentes espaços de coordenadas para os nossos vértices. Este será o nosso primeiro passo para os gráficos 3D!

Leitura Adicional

• Essence of Linear Algebra: grande série de vídeo tutoriais por Grant Sanderson sobre a matemática que envolve transformações e álgebra linear.

Exercícios

• Utilizando a última transformação no objeto, tente trocar a ordem para primeiro rotacionar e, em seguida, transladar. Veja o que acontece e tentar entender por que isso acontece: solução.

• Tente desenhar um segundo objeto com outra chamada para glDrawElements , mas coloque-o em uma posição diferente, utilizando apenas transformações. Certifique-se que este segundo objeto é colocado no canto superior esquerdo da janela e, em vez de girá-lo, escale-o ao longo do tempo (a função sin é útil aqui, note que o uso de sin fará com que o objeto seja invertido assim que uma escala negativa é aplicada): solução.