Teoria
PBR, ou mais comumente conhecido como physically based rendering (renderização baseada em física), é uma coleção de técnicas de renderização mais ou menos baseadas na mesma base teórica que mais se aproxima ao mundo físico. Como a renderização baseada em física visa imitar a luz de maneira fisicamente plausível, geralmente parece mais realista em comparação aos nossos algoritmos de iluminação originais como Phong e Blinn-Phong. Não só parece melhor, pois se aproxima de perto da física real, nós (e especialmente os artistas) podem criar materiais de superfícies baseados em parâmetros físicos sem ter que recorrer a hacks baratos e ajustes para fazer a iluminação parecer certa. Uma das maiores vantagens da criação de materiais baseada em parâmetros físicos é que esses materiais parecerão corretos, independentemente das condições de iluminação; algo que não é verdade em pipelines não-PBR.
A PBR ainda é uma aproximação da realidade (com base nos princípios da física), e é por isso que não é chamado de shading físico, mas physically based shading . Para um modelo de iluminação PBR ser considerado fisicamente baseado, ele deve satisfazer as seguintes 3 condições (não se preocupe, chegaremos a elas em breve):
Ser baseado no modelo de superfície de microfacets ( microfacet surface model ).
Conservar energia.
Utilizar uma BRDF baseada em física.
Nos próximos capítulos PBR, estaremos nos concentrando na abordagem PBR como originalmente explorada pela Disney e adotada para exibição em tempo real pela Epic Games. Sua abordagem, com base no metallic workflow , é decentemente documentada, amplamente adotada nas engines mais populares e parece visualmente incrível. No final desses capítulos, teremos algo que se parece com isso:

Tenha em mente, os tópicos nesses capítulos são bastante avançados, por isso é aconselhável ter uma boa compreensão da OpenGL e iluminação em shader. Alguns dos conhecimentos mais avançados que você precisará para esta série são: frambuffers, cubemaps, correção gama, HDR e normal mapping. Também nos aprofundaremos em algumas matemáticas avançadas, mas farei o meu melhor para explicar os conceitos o mais claro possível.
O Modelo Microfacet
Todas as técnicas PBR são baseadas na teoria dos microfacets . A teoria descreve que qualquer superfície em escala microscópica pode ser descrita por pequenos espelhos reflexivos minúsculos chamados microfacetes . Dependendo da rugosidade de uma superfície, o alinhamento desses pequenos espelhos pode diferir bastante:

Quanto mais áspera uma superfície é, mais caoticamente alinhado será cada microfacet ao longo da superfície. O efeito do alinhamento desses "espelhinhos" minúsculos é que, quando especificamente falando sobre iluminação / reflexão especular, os raios de luz recebidos são mais propensos a se espalhar ( scatter ) ao longo de direções completamente diferentes em superfícies mais ásperas, resultando em uma reflexão especular mais espalhada. Em contraste, em uma superfície lisa, os raios de luz são mais propensos a refletir aproximadamente na mesma direção, nos dando reflexos menores e mais nítidos:

Nenhuma superfície é completamente suave em um nível microscópico, mas visto que esses microfacets são pequenos o suficiente para que não possamos fazer uma distinção entre eles em uma resolução de pixel, nós aproximamos estatisticamente a rugosidade de microfacet da superfície, dado um parâmetro de rugosidade ( roughness ). Com base na aspereza de uma superfície, podemos calcular a proporção de microfacets aproximadamente alinhados a algum vetor $h$. Este vetor $h$ é o halfway vector que fica no meio do caminho entre o vetor de luz $l$ e visão $v$. Discutimos o vetor halfway antes no capítulo de iluminação avançada que é calculado como a soma de $l$ e $v$ dividido pelo seu comprimento:
\[h = \frac{l+v}{\parallel l + v\parallel}\]
Quanto mais os microfacets estão alinhados ao vetor halfway, o mais nítido e mais forte é a reflexão especular. Juntamente com o parâmetro roughness que varia entre 0 e 1, podemos aproximar estatisticamente o alinhamento dos microfacets:

Podemos ver que os valores de rugosidade mais elevados exibem uma forma de reflexão especular muito maior, em contraste com a forma de reflexão especular menor e mais nítida de superfícies lisas.
Conservação de Energia
A aproximação da microfacet emprega uma forma de conservação de energia : a energia da luz de saída nunca deve exceder a energia da luz de entrada (excluindo superfícies emissivas). Olhando para a imagem acima, vemos a área de reflexão especular aumentando, mas também seu brilho diminuindo no aumento dos níveis de roughness. Se a intensidade especular fosse a mesma em cada pixel (independentemente do tamanho da forma especular), as superfícies mais rígidas emitiriam muito mais energia, violando o princípio da conservação de energia. É por isso que vemos reflexos especulares mais intensamente em superfícies lisas e mais vagamente em superfícies ásperas.
Para a conservação de energia se manter, precisamos fazer uma distinção clara entre a luz difusa e especular. No momento em que um raio de luz atinge uma superfície, é dividido em uma parte de refração ( refraction ) e uma parte de reflexão ( reflection ). A parte da reflexão é a luz que é refletida diretamente e não entra na superfície; Isto é o que conhecemos como iluminação especular. A parte de refração é a luz restante que entra na superfície e é absorvida; Isto é o que conhecemos como iluminação difusa.
Há algumas nuances aqui como a luz refratada não é imediatamente absorvida ao tocar a superfície. Da física, sabemos que a luz pode ser modelada como um feixe de energia que continua avançando até perder toda a sua energia; A maneira como um feixe de luz perde energia é por colisão. Cada material consiste em pequenas partículas que podem colidir com o raio de luz, conforme ilustrado na imagem a seguir. As partículas absorvem alguma ou toda, energia da luz em cada colisão que é convertida em calor.
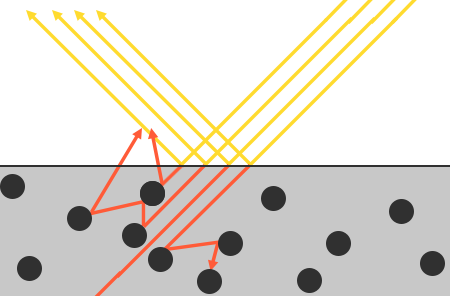
Geralmente, nem toda a energia é absorvida e a luz continuará a dispersar ( scatter ) em uma direção (na maior parte) aleatória de modo que colide com outras partículas até que sua energia seja esgotada ou deixa a superfície novamente. Raios de luz reemergindo da superfície contribuem para a cor observada da superfície (difusa). Em PBR no entanto, fazemos a suposição simplificadora de que toda a luz refratada é absorvida e espalhada a uma pequena área de impacto, ignorando o efeito de raios de luz espalhados que teriam saído da superfície à uma distância. Técnicas de shading específicas que levam isso em conta são conhecidos como técnicas de subsurface scattering que melhoram significativamente a qualidade visual em materiais como pele, mármore ou cera, mas vêm ao preço do desempenho.
Uma sutileza adicional quando se trata de reflexão e refração são superfícies metálicas ( metallic ). As superfícies metálicas reagem diferentemente à luz em comparação a superfícies não metálicas (também conhecidas como dielétricas ( dielectrics )). Superfícies metálicas seguem os mesmos princípios de reflexão e refração, mas toda a luz refratada fica diretamente absorvida sem dispersão. Isso significa que as superfícies metálicas só deixam sair a luz refletida ou especular; Superfícies metálicas não mostram cores difusas. Devido a essa aparente distinção entre metais e dielétricos, ambos são tratados de maneira diferente no pipeline PBR que vamos aprofundar mais no capítulo.
Essa distinção entre a luz refletida e refratada nos leva a outra observação em relação à preservação da energia: elas são mutuamente exclusivas. Qualquer energia de luz que é refletida, não será mais absorvida pelo próprio material. Assim, a energia deixada para entrar na superfície, como luz refratada é diretamente a energia resultante depois que cuidamos da reflexão.
Preservamos essa relação de conservação de energia, primeiro calculando a fração especular que acumula a porcentagem de energia da luz de entrada que é refletida. A fração de luz refratada é então calculada diretamente a partir da fração especular como:
float kS = calculateSpecularComponent(...); // reflection/specular fraction
float kD = 1.0 - kS; // refraction/diffuse fraction
Desta forma, sabemos tanto a quantidade de luz recebida que é refletida e a quantidade de luz recebida que é refrata, aderindo ao mesmo tempo ao princípio da conservação de energia. Dada esta abordagem, é impossível para a contribuição refratada / difusa e refletida / especular de exceder 1.0, garantindo assim que a soma de sua energia nunca exceda a energia de luz recebida. Algo que não levamos em conta nos capítulos de iluminação anteriores.
A Equação de Refletância
Isso nos leva a algo chamado de render equation, uma equação elaborada por algumas pessoas muito inteligentes, que atualmente é o melhor modelo que temos para simular as aparências da luz. O PBR segue fortemente uma versão mais especializada da render equation conhecida como a equação de refletância ( reflectance equation ). Para entender adequadamente o PBR, é importante primeiro construir uma sólida compreensão da equação de refletância:
\[L_o(p,\omega_o)=\int_\Omega f_r(p,\omega_i,\omega_o)L_i(p,\omega_i)n\cdot\omega_id\omega_i\]
A equação de reflectância parece assustadora a primeira vista, mas ao dissecá-la, você verá que ela faz sentido. Para entender a equação, temos que nos aprofundar em um pouco de radiometria ( radiometry ). A radiometria é a medição da radiação eletromagnética, incluindo a luz visível. Existem várias quantidades radiométricas que podemos usar para medir a luz sobre superfícies e direções, mas só discutiremos uma única quantidade que é relevante para a equação de refletância conhecida como radiância ( radiance ), denotada aqui como $L$. A radiância é usada para quantificar a magnitude ou a força da luz que vem de uma única direção. É um pouco complicado entender a princípio já que a radiância é na verdade uma combinação de várias quantidades físicas, então vamos nos concentrar nelas primeiro:
Fluxo radiante ( radiant flux ): o fluxo radiante $\Phi$ é a energia transmitida de uma fonte de luz medida em Watts. A luz é uma soma coletiva de energia sobre vários comprimentos de onda diferentes, cada comprimento de onda associado a uma cor específica (visível). A energia emitida de uma fonte de luz pode, portanto, ser pensada como uma função de todos os seus diferentes comprimentos de onda. Comprimentos de onda entre 390nm a 700nm (nanômetros) são considerados parte do espectro de luz visível, isto é, os comprimentos de onda que o olho humano é capaz de perceber. Abaixo você encontrará uma imagem das diferentes energias por comprimento de onda da luz do dia:
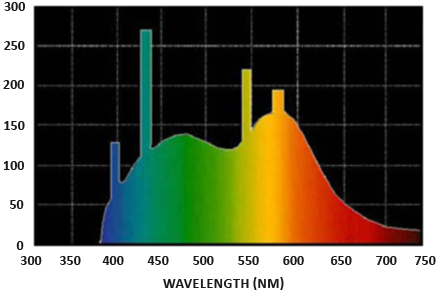
O fluxo radiante mede a área total dessa função de diferentes comprimentos de onda. Tomando diretamente essa medida de comprimentos de onda como entrada é ligeiramente impraticável, portanto normalmente simplificamos a representação do fluxo radiante, não como uma função de diferentes forças de comprimento de onda, mas como uma tupla de cores de luz codificada como RGB (ou como costumávamos chamá-la: cor de luz). Essa codificação traz bastante perda de informação, mas isso geralmente é insignificante para aspectos visuais.
Solid angle: O solid angle, denotado como $\omega$, nos diz o tamanho ou área de uma forma projetada sob uma esfera unitária. A área da forma projetada nesta esfera unitária é conhecida como solid angle ; Você pode visualizar o solid angle como uma direção com o volume:
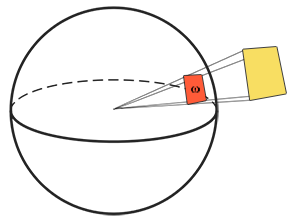
Pense como um observador no centro desta esfera olhando na direção da forma; O tamanho da silhueta que enxerga é o solid angle.
Intensidade radiante ( radiant intensity ): a intensidade radiante mede a quantidade de fluxo radiante por solid angle, ou a força de uma fonte de luz sobre uma área projetada em uma esfera unitária. Por exemplo, dada uma luz omnidirecional que irradia igualmente em todas as direções, a intensidade radiante pode nos dar sua energia sobre uma área específica (solid angle):
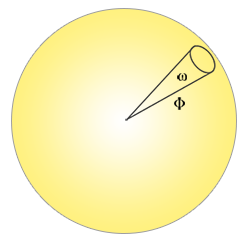
A equação para descrever a intensidade radiante é definida da seguinte forma:
\[I=\frac{d\Phi}{d\omega}\]
Onde $I$ é o fluxo radiante $\Phi$ sobre o solid angle $\omega$.
Com conhecimento de fluxo radiante, intensidade radiante e solid angle, podemos finalmente descrever a equação para a radiância ( radiance ). A radiância é descrita como a energia total observada em uma área $A$ sobre o solid angle $\omega$ de uma luz de intensidade radiante $\Phi$:
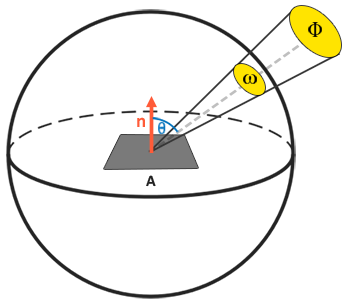
A radiância é uma medida radiométrica da quantidade de luz em uma área, escalada pelo ângulo incidente (ou de chegada) $\theta$ da luz para a superfície normal como $cos \theta$: a luz é mais fraca a medida que menos irradia diretamente para a superfície, e mais forte quanto mais é diretamente perpendicular à superfície. Isso é semelhante à nossa percepção de iluminação difusa do capítulo de iluminação básica como $cos \theta$ corresponde diretamente ao produto escalar entre o vetor de direção da luz e a normal da superfície:
float cosTheta = dot(lightDir, N);
A equação de radiância é bastante útil, pois contém mais quantidades físicas em que estamos interessados. Se considerarmos o solid angle $\omega$ e a área $A$ sendo infinitamente pequenos, podemos usar a radiância para medir o fluxo de um único raio de luz batendo em um único ponto no espaço. Essa relação permite calcular o brilho de um único raio de luz que influencia um único ponto (de fragmento); Nós efetivamente traduzimos o solid angle $\omega$ em um vector de direção $\omega$ e $A$ em um ponto $p$. Dessa forma, podemos usar diretamente a radiância em nossos shaders para calcular a contribuição de um único raio de luz por fragmento.
De fato, quando se trata de radiância, geralmente nos importamos com toda a luz recebida em um ponto $p$, que é a soma de toda a radiância conhecida como irradiância ( irradiance ). Com conhecimento de ambas a radiância e irradiância, podemos voltar à equação de refletância:
\[L_o(p,\omega_o)=\int_\Omega f_r(p,\omega_i,\omega_o)L_i(p,\omega_i)n\cdot\omega_id\omega_i\]
Sabemos agora que $L$ na render equation representa a radiância de algum ponto $p$ e algum solid angle incidente infinitamente pequeno $\omega_i$ que pode ser considerado como um vetor de direção de incidência $\omega_i$. Lembre-se que $cos$ $\theta$ escala a energia com base no ângulo de incidência da luz na superfície, que encontramos na equação de reflectância como $n \cdot \omega_i$. A equação de refletância calcula a soma da radiância refletida $L_o(p, \omega_o)$ de um ponto $p$ na direção $\omega_o$, que é a direção de saída para o observador. Em outras palavras: $L_o$ mede a soma refletida da irradiância das luzes no ponto $p$ observada de $\omega_o$.
A equação de reflectância é baseada em torno da irradiância, que é a soma de toda a radiância recebida que medimos da luz. Não apenas de uma única direção de luz recebida, mas de todas as incidências de luz dentro de um hemisfério $\Omega$ centrada em torno do ponto $p$. Um hemisfério pode ser descrito como a meia esfera alinhada em torno de uma normal de superfície $n$:
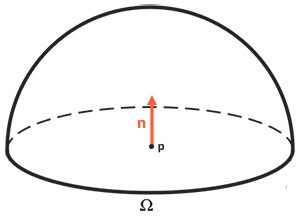
Para calcular o total de valores dentro de uma área ou (no caso de um hemisfério) um volume, usamos uma construção matemática chamada integral denotada na equação de refletância como $\int$ sobre todas as direções de incidência $d\omega_i$ dentro do hemisfério $\Omega$. Uma integral mede a área de uma função, que pode ser calculada analiticamente ou numericamente. Como não há solução analítica para a equação de renderização e de reflexão, vamos ter que resolver numericamente a integral discretamente. Isso se traduz em tomar o resultado de pequenos passos discretos da equação de refletância sobre o hemisfério $\Omega$ e calcular os resultados sobre o tamanho do passo. Isso é conhecido como a soma de Riemann que podemos visualizar no código da seguinte forma:
int steps = 100;
float sum = 0.0f;
vec3 P = ...;
vec3 Wo = ...;
vec3 N = ...;
float dW = 1.0f / steps;
for(int i = 0; i < steps; ++i)
{
vec3 Wi = getNextIncomingLightDir(i);
sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW;
}
Ao dimensionar os passos por dW, a soma será igual à área total ou volume da função integral. Como dW escala cada passo discreto, este pode ser pensado como $d\omega_i$ na equação de reflectância. Matematicamente $d \omega_i$ é o símbolo contínuo sobre o qual calculamos a integral e, embora não se relacione diretamente com o dW no código (já que este é um passo discreto da soma de Riemann), ajuda a pensar nisso desta maneira. Tenha em mente que tomar medidas discretas sempre nos dará uma aproximação da área total da função. Um leitor cuidadoso perceberá que podemos aumentar a precisão da soma do Riemann, aumentando o número de passos.
A equação de reflectância soma a radiância de todas as direções de luzes incidentes $\omega_i$ sobre o hemisfério $\Omega$ dimensionada por $f_r$ que atingem o ponto $p$ e retorna a soma da luz refletida $L_o$ na direção do observador. A radiância recebida pode vir de fontes de luz, como estamos familiarizados ou de um environment map medindo a radiância de todas as direções incidentes, como vamos discutir nos capítulos de IBL.
Agora, a única parte desconhecida que resta é o símbolo $f_r$ conhecido como a função de distribuição reflexiva bidirecional BRDF ( bidirectional reflective distribution function ) que escala ou pesa a radiância recebida com base nas propriedades do material da superfície.
BRDF
A BRDF
, ou bidirectional reflective distribution function
, é uma função que recebe como entrada a direção de incidência (luz) $\omega_i$, a direção de saída (observador) $\omega_o$, a normal da superfície $n$ e um parâmetro de superfície $a$ que representa a rugosidade do micro-superfície. A BRDF aproxima o quanto cada raio individual de luz $\omega_i$ contribui para a luz final refletida de uma superfície opaca, dadas suas propriedades materiais. Por exemplo, se a superfície for perfeitamente lisa (~ como um espelho), a função BRDF retornaria 0.0 para todos os raios de luz incidentes $\omega_i$, exceto o único raio que tem o mesmo ângulo (refletido) como o raio de reflexão $\omega_o$ em que a função retorna 1.0.
Uma BRDF aproxima as propriedades reflexivas e refrativas do material com base na teoria de microfacet discutida anteriormente. Para uma BRDF ser fisicamente plausível, precisa que respeitar a lei da conservação de energia, isto é, a soma de luz refletida nunca deve exceder a quantidade de luz incidente. Tecnicamente, Blinn-Phong é considerado uma BRDF que toma o mesmo $\omega_i$ e $\omega_o$ como entradas. No entanto, Blinn-Phong não é considerado ser fisicamente baseado já que não adere ao princípio da conservação de energia. Existem várias BRDFs baseadas em física para aproximar a reação da superfície à luz. No entanto, quase todos os pipelines de renderização de PBR em tempo real usam uma BRDF conhecido como a Cook-Torrance BRDF .
A Cook-Torrance BRDF contém uma parte difusa e uma parte especular:
\[f_r=k_df_{lambert} + k_sf_{cook-torrance}\]
Aqui $k_d$ é a relação anterior mencionada de energia da luz incidente que é refratada com $k_s$ sendo a proporção refletida. O lado esquerdo da BRDF afirma a parte difusa da equação denotada aqui como $f_{Lambert}$. Isso é conhecido como Lambertian semelhante ao que usamos para diffuse shading, que é um fator constante denotado como:
\[f_{lambert}=\frac{c}{\pi}\]
Com $c$ sendo o albedo ou cor da superfície (pense na textura de superfície difusa). A divisão por $\pi$ está lá para normalizar a luz difusa, já que a integral anterior que contém a BRDF é dimensionada por $\pi$ (chegaremos a isso nos capítulos de IBL).
Você pode se perguntar como esse Lambertian diffuse se relaciona com a iluminação difusa que usamos antes: a cor da superfície multiplicada pelo produto escalar entre a normal da superfície e a direção da luz. O produto escalar ainda está lá, mas saiu da BRDF como encontramos $n \cdot \omega_i$ no final da integral $L_o$.
Existem diferentes equações para a parte difusa da BRDF, que tendem a parecer mais realistas, mas também são mais custosas computacionalmente. Como concluído pela Epic Games, no entanto, o Lambertian diffuse é suficiente para a maioria dos propósitos de renderização em tempo real.
A parte especular da BRDF é um pouco mais avançada e é descrita como:
\[f_{CookTorrance}=\frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)}\]
A BRDF especular de Cook-Torrance é composta de três funções e um fator de normalização no denominador. Cada um dos símbolos $D$, $F$ e $G$ representam um tipo de função que aproxima uma parte específica das propriedades reflexivas da superfície. Estes são definidos como a função de Distribuição normal, a equação de Fresnel e a função de Geometria:
Função de distribuição normal: aproxima o quanto os microfacets da superfície estão alinhados ao vetor halfway, influenciada pela rugosidade da superfície; Esta é a função principal que aproxima os microfacets.
Função da geometria: descreve a propriedade de auto-sombreamento dos microfacets. Quando uma superfície é relativamente áspera, os microfacets da superfície podem ofuscar outros microfacets reduzindo a luz que a superfície reflete.
Equação de Fresnel: A equação de Fresnel descreve a proporção de reflexão da superfície em diferentes ângulos de superfície.
Cada uma dessas funções é uma aproximação de seus equivalentes físicos e você encontrará mais de uma versão de cada uma que visa aproximar a física de maneiras diferentes; alguns mais realistas, outros mais eficientes. É perfeitamente normal escolher qualquer versão aproximada dessas funções que você deseja usar. Brian Karis da Epic Games fez uma grande pesquisa sobre os vários tipos de aproximações aqui. Nós vamos escolher as mesmas funções usadas pela Unreal Engine 4 da Epic Games que são: Trowbridge-Reitz GGX para D, a aproximação de Fresnel-Schlick para F, e o Schlick-GGX de Smith para G.
Função de Distribuição Normal (NDF)
A função de distribuição normal $D$ aproxima estatisticamente a área de superfície relativa de microfacets exatamente alinhados ao vetor (halfway) $h$. Há uma infinidade de NDFs que aproximam estatisticamente do alinhamento geral dos microfacets dado algum parâmetro de rugosidade. O que estaremos usando é conhecido como o Trowbridge-Reitz GGX:
\[NDF_{GGXTR}(n,h,\alpha)=\frac{\alpha^2}{\pi((n\cdot h)^2(\alpha^2-1)+1)^2}\]
Aqui $h$ é o vetor halfway para medir contra os microfacets da superfície, com $\alpha$ sendo uma medida da aspereza da superfície. Se tomarmos $h$ como o vetor halfway entre a normal da superfície e a direção da luz variando os parâmetros de rugosidade, recebemos o seguinte resultado visual:

Quando a rugosidade é baixa (assim a superfície é suave), um número altamente concentrado de microfacets está alinhado a vetores halfway sobre um raio pequeno. Devido a esta alta concentração, a NDF exibe um ponto muito brilhante. Em uma superfície áspera no entanto, onde os microfacets estão alinhados em direções muito mais aleatórias, você encontrará um número muito maior de vetores halfway $h$ um meramente alinhados aos microfacets (mas menos concentrados), nos dando os resultados mais acinzentados .
Em GLSL, a função de distribuição normal Trowbridge-Reitz GGX é traduzida para o seguinte código:
float DistributionGGX(vec3 N, vec3 H, float a)
{
float a2 = a*a;
float NdotH = max(dot(N, H), 0.0);
float NdotH2 = NdotH*NdotH;
float nom = a2;
float denom = (NdotH2 * (a2 - 1.0) + 1.0);
denom = PI * denom * denom;
return nom / denom;
}
Função de Geometria
A função de geometria aproxima estatisticamente a área de superfície relativa, onde seus micro detalhes de superfície se auto obstruem, fazendo com que os raios de luz sejam ocluídos.
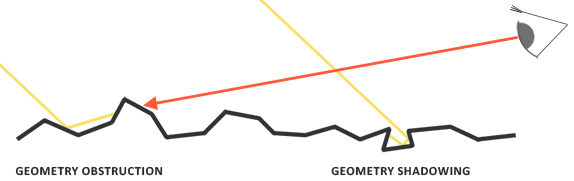
Semelhante ao NDF, a função de geometria recebe o parâmetro de rugosidade de um material como entrada, com superfícies mais rígidas tendo uma maior probabilidade de ocluir microfacets. A função de geometria que usaremos é uma combinação da aproximação GGX e Schlick-Beckmann conhecida como Schlick-GGX:
\[G_{SchlickGGX}(n,v,k)=\frac{n\cdot v}{(n\cdot v}(1-k) + k\]
Aqui $k$ é um remapeamento de $\alpha$ com base em se estamos usando a função de geometria para iluminação direta ou iluminação IBL:
\[k_{direct}=\frac{(\alpha + 1)^2}{8}\]
\[k_{IBL}=\frac{\alpha^2}{2}\]
Observe que o valor de $\alpha$ pode ser diferente com base em como seu mecanismo traduz a rugosidade $\alpha$. Nos capítulos a seguir, discutiremos extensivamente como e onde esse remapeamento se torna relevante.
Para efetivamente aproximar a geometria, precisamos levar em conta tanto a direção do observador (obstrução da geometria) quanto o vetor de direção da luz (sombreamento de geometria). Podemos levar ambos em conta usando o método de Smith :
\[G(n,v,l,k)=G_{sub}(n,v,k)G_{sub}(n,l,k)\]
Usando o método de Smith com Schlick-GGX como $G_{sub}$ fornece a seguinte aparência visual variando-se a rugosidade R:

A função de geometria é um multiplicador entre [0.0, 1.0] com 1.0 (ou branco) medindo nenhum sombreamento de microfacet, e 0.0 (ou preto), sombreamento completo de microfacet.
Em GLSL, a função de geometria se traduz no seguinte código:
float GeometrySchlickGGX(float NdotV, float k)
{
float nom = NdotV;
float denom = NdotV * (1.0 - k) + k;
return nom / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
{
float NdotV = max(dot(N, V), 0.0);
float NdotL = max(dot(N, L), 0.0);
float ggx1 = GeometrySchlickGGX(NdotV, k);
float ggx2 = GeometrySchlickGGX(NdotL, k);
return ggx1 * ggx2;
}
Equação de Fresnel
A equação de Fresnel (pronunciada como freh-nel) descreve a proporção de luz que se reflete sobre a luz que é refratada, o que varia sobre o ângulo que estamos olhando para uma superfície. No momento em que a luz atinge uma superfície, com base no ângulo da superfície com a vista, a equação de Fresnel nos diz a porcentagem de luz que se reflete. A partir dessa proporção de reflexão e do princípio da conservação de energia, podemos obter diretamente a porção refratada da luz.
Cada superfície ou material tem um nível de refletividade base ( base reflectivity ) quando olhamos diretamente para sua superfície, mas ao olhar para a superfície de um ângulo, todas as reflexões se tornam mais aparentes em comparação com a refletividade base da superfície. Você pode verificar isso por si mesmo olhando para a sua mesa (presumivelmente) de madeira / metálica que tem um certo nível de refletividade base de um ângulo de visão perpendicular, mas olhando para sua mesa de um ângulo de quase 90 graus, você verá as reflexões muito mais aparentes. Todas as superfícies teoricamente refletem totalmente a luz se vistas de ângulos perfeitos de 90 graus. Este fenômeno é conhecido como Fresnel e é descrito pela equação de Fresnel.
A equação de Fresnel é uma equação bastante complexa, mas felizmente pode ser aproximada usando a aproximação Fresnel-Schlick:
\[F_{Schlick}(h,v,F_0)=F_0+(1-F_0)(1-(h\cdot v))^5\]
$F_0$ representa a refletividade base da superfície, que calculamos usando algo chamado os índices de refração ou IOR. Como você pode ver em uma superfície de esfera, quanto mais olhamos para os ângulos rasos da superfície (com o ângulo entre os vetores halfway e do observador atingindo 90 graus), mais forte o Fresnel e, portanto, as reflexões:

Existem algumas sutilezas envolvidas com a equação de Fresnel. Uma é que a aproximação Fresnel-Schlick só é realmente definida para superfícies dielétricas ou não metálicas. Para superfícies condutoras (metais), o cálculo da refletividade base com índices de refração não se mantém adequadamente e precisamos usar uma equação de fresnel diferente para os condutores. Como isso é inconveniente, aproximamos ainda mais pela pré-computação da resposta da superfície em incidência normal ($F_0$) em um ângulo de 0 grau como se estivesse olhando diretamente em uma superfície. Nós interpolamos esse valor com base no ângulo de visão, conforme a aproximação Fresnel-Schlick, de modo que podemos usar a mesma equação para metais e não-metais.
A resposta da superfície em incidência normal, ou a refletividade base, pode ser encontrada em grandes bancos de dados, como estes com alguns dos valores mais comuns listados abaixo, conforme tirado das notas do curso de Naty Hoffman:
| Material | $F_0$(Linear) | $F_0$(sRGB) | Cor |
|---|---|---|---|
| Water | $(0.02, 0.02, 0.02)$ | $(0.15, 0.15, 0.15)$ | |
| Plastic / Glass (Low) | $(0.03, 0.03, 0.03)$ | $(0.21, 0.21, 0.21)$ | |
| Plastic High | $(0.05, 0.05, 0.05)$ | $(0.24, 0.24, 0.24)$ | |
| Glass (high) / Ruby | $(0.08, 0.08, 0.08)$ | $(0.31, 0.31, 0.31)$ | |
| Diamond | $(0.17, 0.17, 0.17)$ | $(0.45, 0.45, 0.45)$ | |
| Iron | $(0.56, 0.57, 0.58)$ | $(0.77, 0.78, 0.78)$ | |
| Copper | $(0.95, 0.64, 0.54)$ | $(0.98, 0.82, 0.76)$ | |
| Gold | $(1.00, 0.71, 0.29)$ | $(1.00, 0.86, 0.57)$ | |
| Aluminium | $(0.91, 0.92, 0.92)$ | $(0.96, 0.96, 0.97)$ | |
| Silver | $(0.95, 0.93, 0.88)$ | $(0.98, 0.97, 0.95)$ | |
O que é interessante de observar aqui é que, para todas as superfícies dielétricas, a refletividade base nunca fica acima de 0.17, que é a exceção, em vez da regra, enquanto para os condutores a refletividade base é muito maior e (principalmente) varia entre 0.5 e 1.0. Além disso, para condutores (ou superfícies metálicas) a refletividade base é colorida. É por isso que $F_0$ é apresentado como uma tupla RGB (a refletividade na incidência normal pode variar por comprimento de onda); Isso é algo que só vemos em superfícies metálicas.
Esses atributos específicos de superfícies metálicas em comparação com superfícies dielétricas deu origem a algo chamado metallic workflow . No metallic workflow, nós configuramos os materiais das superfícies com um parâmetro extra conhecido como metalness que descreve se uma superfície é uma superfície metálica ou não metálica.
Teoricamente, o metalness de um material é binário: o material é um metal ou não é; Não pode ser ambos. No entanto, a maioria dos pipelines de renderização permitem a configuração do metalness de uma superfície linearmente entre 0.0 e 1.0. Isso é principalmente por causa da falta de precisão de textura do material. Por exemplo, uma superfície com pequenas partículas / arranhões de pó / areia (não metal) sobre uma superfície metálica é difícil de renderizar com valores de metalness binários.
Ao pré-computar $F_0$ para ambos os dielétricos e condutores, podemos usar a mesma aproximação de Fresnel-Schlick para ambos os tipos de superfícies, mas temos que tingir a refletividade base se tivermos uma superfície metálica. Geralmente, conseguimos isso da seguinte forma:
vec3 F0 = vec3(0.04);
F0 = mix(F0, surfaceColor.rgb, metalness);
Definimos uma refletividade base que é aproximada para a maioria das superfícies dielétricas. Esta é mais uma aproximação como $F_0$ é calculada em torno de dielétricos mais comuns. Uma refletividade base de 0.04 se mantém para a maioria dos dielétricos e produz resultados fisicamente plausíveis sem ter que criar um parâmetro de superfície adicional. Em seguida, com base em quão metálica uma superfície é, tomamos a refletividade base dielétrica ou tomamos $F_0$ criadas como a cor da superfície. Como as superfícies metálicas absorvem toda a luz refratada, elas não têm reflexões difusas e podemos usar diretamente a textura de cor de superfície como sua refletividade base.
No código, a aproximação de Fresnel Schlick se traduz em:
vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}
Com a cosTheta sendo o resultado do produto escalar entre a direção normal $n$ e a direção halfway $h$ (ou de vista $v$).
Equação de Refletância Cook-Torrance
Com cada componente da BRDF Torrance do Cook descrita, podemos incluir a BRDF baseada em física na equação de reflectância final agora:
\[L_0(p,\omega_o)=\int_\Omega(k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)})L_i(p,\omega_i)n\cdot\omega_i d\omega_i\]
Esta equação não é matematicamente totalmente correta no entanto. Você pode lembrar que o termo Fresnel $F$ representa a proporção de luz que é refletida de uma superfície. Isso é efetivamente nossa relação $k_s$, o que significa que a parte (BRDF) especular da equação de refletância contém implicitamente a relação de reflectância $k_s$. Dado isso, nossa equação final de refletância final torna-se:
\[L_0(p,\omega_o)=\int_\Omega(k_d\frac{c}{\pi} + \frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)})L_i(p,\omega_i)n\cdot\omega_i d\omega_i\]
Essa equação agora descreve completamente um modelo de renderização fisicamente baseado que é geralmente reconhecido como o que comumente entendemos como renderização baseada em física, ou PBR. Não se preocupe se você ainda não entendeu completamente como precisaremos adequar todas as matemáticas discutidas no código. Nos próximos capítulos, vamos explorar como utilizar a equação de refletância para obter resultados muito mais fisicamente plausíveis em nossa iluminação renderizada e todos os pedacinhos devem começar lentamente a se encaixar.
Criando (Authoring) Materiais PBR
Com o conhecimento do modelo matemático subjacente de PBR, finalizaremos a discussão descrevendo como os artistas geralmente criam as propriedades físicas de uma superfície com as quais podemos alimentar diretamente as equações da PBR. Cada um dos parâmetros da superfície que precisamos para um pipeline PBR pode ser definido ou modelado por texturas. O uso de texturas nos dá controle por fragmento sobre como cada ponto de superfície específico deve reagir à luz: se esse ponto é metálico, áspero ou suave, ou como a superfície responde a diferentes comprimentos de onda.
Abaixo, você verá uma lista de texturas que você frequentemente encontrará em um pipeline PBR junto com sua saída visual, se fornecida a um renderizador de PBR:

Albedo: A textura de albedo ( albedo texture ) especifica para cada texel a cor da superfície, ou a refletividade base se esse texel é metálico. Isso é muito semelhante ao que usamos antes como uma textura difusa, mas todas as informações de iluminação são extraídas da textura. Texturas difusas muitas vezes têm ligeiras sombras ou fendas escuras dentro da imagem que é algo que você não quer em uma textura de albedo; Deve-se conter apenas as cores (ou coeficientes de absorção refratados) da superfície.
Normal: A textura do mapa de normais ( normal map texture ) é exatamente como usamos antes no capítulo mapeamento de normais. O mapa de normais nos permite especificar, por fragmento, uma normal única para dar a ilusão de que uma superfície é mais curvada ( bumpier ) do que sua contraparte plana.
Metálico: O mapa metálico ( metallic map ) especifica por texel se um texel é metálico ou não é. Com base em como o motor PBR é configurado, os artistas podem criar o metalness tanto com valores de cinza ou com valores binários de preto ou branco.
Rugosidade: O mapa de rugosidade ( roughness map
) especifica o quão áspero uma superfície é para cada texel. O valor de rugosidade amostrado da rugosidade influencia as orientações estatísticas de microfacets da superfície. Uma superfície mais áspera recebe reflexões mais amplas e borradas, enquanto uma superfície lisa é focada e reflexões bem definidas. Alguns motores PBR esperam um mapa de suavidade ( smoothness map
) em vez de um mapa de rugosidade que alguns artistas acham mais intuitivo. Esses valores são então traduzidos (1,0 - smoothness) para aspereza no momento em que eles são amostrados.
AO: A oclusão ambiente ( ambient occlusion ) ou mapa AO especifica um fator de sombreamento extra da superfície e geometrias potencialmente próximas. Se tivermos uma superfície de tijolo, por exemplo, a textura do albedo não deve ter informações de sombreamento dentro das fendas do tijolo. O mapa do AO, no entanto, especifica essas bordas escuras, pois é mais difícil para a luz escapar. Tomar a oclusão ambiente em conta no final do estágio de iluminação pode aumentar significativamente a qualidade visual de sua cena. O mapa de oclusão ambiente de uma malha / superfície é gerado manualmente ou pré-calculado em programas de modelagem 3D.
Artistas definem e ajustam esses valores de entrada fisicamente baseados em uma base por texel e podem basear seus valores de textura nas propriedades da superfície física dos materiais do mundo real. Esta é uma das maiores vantagens de um pipeline de renderização do PBR, uma vez que essas propriedades físicas de uma superfície permanecem as mesmas, independentemente do ambiente ou configuração de iluminação, facilitando a vida para os artistas obterem resultados fisicamente plausíveis. As superfícies criadas em um pipeline PBR podem ser facilmente compartilhadas entre os diferentes motores de renderização da PBR, e ficarão corretos, independentemente do ambiente em que estão e, como resultado, parecerão muito mais naturais.
Leitura Adicional
"Background: Physics and Math of Shading" por Natur Hoffmann: Há muita teoria para discutir plenamente em um único artigo, logo a teoria aqui mal arranha sua superfície; Se você quiser saber mais sobre a física da luz e como esta se refere à teoria do PBR, este é o recurso que você deseja ler.
Real Shading in Unreal Engine 4: discute o modelo PBR adotado pela Epic Games em sua 4ª versão da Unreal Engine. O sistema PBR que nos concentraremos nestes capítulos é baseado neste modelo de PBR.
"SH17C Physically Based Shading" por knarkowicz: Grande showcase de todos os elementos individuais de PBR em uma demo interativa do Shadertoy.
Marmoset: PBR Theory: uma introdução à PBR principalmente destinada a artistas, mas, no entanto, uma boa leitura.
Coding Labs: Physically based rendering: uma introdução à equação de renderização e como se refere ao PBR.
Coding Labs: Physically Based Rendering - Cook–Torrance: uma introdução ao cozinheiro-torrance BRDF.
Wolfire Games - Physically based rendering: uma introdução ao PBR por Lukas Orsvärn.