Iluminação

Post Original

No capítulo anterior, lançamos os fundamentos para se construir um renderizador realista baseado em física. Neste capítulo, vamos nos concentrar em traduzir a teoria discutida anteriormente em um renderizador real que usa fontes de luz diretas (ou analíticas): pense em luzes pontuais, luzes direcionais e / ou holofotes ( spotlights ).

Vamos começar revisitando a equação final de refletância do capítulo anterior:

\[L_o(p,\omega_o)=\int_\Omega(k_d\frac{c}{\pi}+\frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)})L_i(p,\omega_i)n\cdot \omega_i d\omega_i\]

Agora sabemos principalmente o que está acontecendo, mas o que ainda permaneceu uma grande incógnita é como exatamente vamos representar a irradiância, a radiância total $L$, da cena. Sabemos que a radiância $L$ (conforme interpretada na computação gráfica) mede o fluxo radiante $\phi$ ou a energia da luz de uma fonte de luz sobre um determinado solid angle $\omega$. No nosso caso, assumimos que o solid angle $\omega$ é infinitamente pequeno, caso em que a radiância mede o fluxo de uma fonte de luz sobre um único raio de luz ou vetor de direção.

Dado esse conhecimento, como traduzimos isso em parte do conhecimento de iluminação que acumulamos nos capítulos anteriores? Bem, imagine que temos um único ponto de luz (uma fonte de luz que brilha igualmente em todas as direções) com um fluxo radiante de (23.47, 21.31, 20.79) traduzido para um valor RGB. A intensidade radiante desta fonte de luz é igual ao seu fluxo radiante em todos os raios de direção de saída. No entanto, ao analisar um ponto específico $p$ em uma superfície, de todas as direções de luz de entrada possíveis sobre seu hemisfério $\Omega$, apenas um vetor de direção de entrada $w_i$ vem diretamente da fonte de luz pontual. Como temos apenas uma única fonte de luz em nossa cena, assumida como um único ponto no espaço, todas as outras direções de luz de entrada possíveis têm radiância zero observada sobre o ponto da superfície $p$:

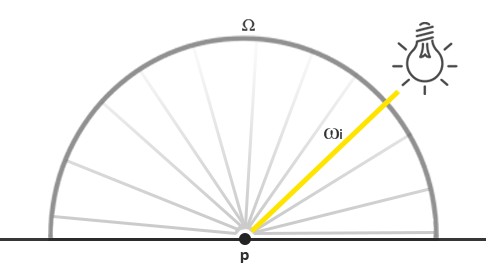
Se, a princípio, assumirmos que a atenuação da luz (escurecimento da luz ao longo da distância) não afeta a fonte de luz pontual, a radiância do raio de luz que entra é a mesma, independentemente de onde posicionamos a luz (excluindo a escala da radiância pelo ângulo de incidência $\cos theta$). Isso porque a luz pontual tem a mesma intensidade radiante independentemente do ângulo que olhamos para ela, modelando efetivamente sua intensidade radiante como seu fluxo radiante: um vetor constante (23.47, 21.31, 20.79).

No entanto, a radiância também assume uma posição $p$ como entrada e como qualquer fonte de luz pontual realista leva em conta a atenuação da luz, a intensidade radiante da fonte de luz pontual é dimensionada por alguma medida da distância entre o ponto $p$ e a fonte de luz. Então, conforme extraído da equação de radiância original, o resultado é escalado pelo produto escalar entre a normal da superfície $n$ e a direção da luz que entra $w_i$.

Para colocar isso em termos mais práticos: no caso de uma luz pontual direta, a função de radiância $L$ mede a cor da luz, atenuada ao longo de sua distância para $p$ e dimensionada por $n \cdot w_i$ , mas apenas sobre o único raio de luz $w_i$ que atinge $p$ que é igual ao vetor de direção da luz de $p$. No código, isso se traduz em:

vec3  lightColor  = vec3(23.47, 21.31, 20.79);
vec3  wi          = normalize(lightPos - fragPos);
float cosTheta    = max(dot(N, Wi), 0.0);
float attenuation = calculateAttenuation(fragPos, lightPos);
vec3  radiance    = lightColor * attenuation * cosTheta;

Apesar da terminologia diferente, este trecho de código deve ser bastante familiar para você: é exatamente assim que temos feito a iluminação difusa até agora. Quando se trata de iluminação direta, a radiância é calculada de forma semelhante a como calculamos a iluminação antes, pois apenas um único vetor de direção da luz contribui para a radiância da superfície.

Para outros tipos de fontes de luz originadas de um único ponto, calculamos a radiância de forma semelhante. Por exemplo, uma fonte de luz direcional tem uma constante $w_i$ sem um fator de atenuação. E um holofote não teria uma intensidade radiante constante, mas uma que é dimensionada pelo vetor de direção direta do holofote.

Isso também nos traz de volta à integral $\int$ sobre o hemisfério da superfície $\Omega$. Como sabemos de antemão as localizações únicas de todas as fontes de luz contribuintes ao shading de um único ponto da superfície, não é necessário tentar resolver a integral. Podemos tomar diretamente o número (conhecido) de fontes de luz e calcular sua irradiância total, visto que cada fonte de luz tem apenas uma única direção de luz que influencia no brilho da superfície. Isso torna o PBR em fontes de luz direta relativamente simples, pois efetivamente só precisamos fazer um loop sobre as fontes de luz contribuintes. Quando mais tarde levarmos em consideração a iluminação do ambiente nos capítulos IBL, teremos que levar em consideração a integral, pois a luz pode vir de qualquer direção.

Um modelo de superfície PBR

Vamos começar escrevendo um shader de fragmento que implementa os modelos PBR descritos anteriormente. Primeiro, precisamos pegar as entradas relevantes ao PBR para o shading da superfície:

#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;
  
uniform vec3 camPos;
  
uniform vec3  albedo;
uniform float metallic;
uniform float roughness;
uniform float ao;

Usamos as entradas padrão calculadas de um shader de vértice genérico e um conjunto de constantes de propriedades de material da superfície do objeto.

Então, no início do shader de fragmento fazemos os cálculos usuais exigidos por qualquer algoritmo de iluminação:

void main()
{
    vec3 N = normalize(Normal); 
    vec3 V = normalize(camPos - WorldPos);
    [...]
}

Iluminação Direta

No exemplo de demonstração deste capítulo temos um total de 4 luzes pontuais que, em conjunto, representam a irradiância da cena. Para satisfazer a equação de refletância, iteramos sobre as fontes de luz, calculamos cada radiância individual e somamos sua contribuição escalada pela BRDF e o angulo de incidência da luz. Podemos pensar nesse loop como a resolução da integral $\int$ sobre $\Omega$ para fontes de luz direta. Primeiro, calculamos todas variáveis relevantes para cada luz:

vec3 Lo = vec3(0.0);
for(int i = 0; i < 4; ++i) 
{
    vec3 L = normalize(lightPositions[i] - WorldPos);
    vec3 H = normalize(V + L);
  
    float distance    = length(lightPositions[i] - WorldPos);
    float attenuation = 1.0 / (distance * distance);
    vec3 radiance     = lightColors[i] * attenuation; 
    [...]  

Ao calcular a iluminação no espaço linear (fazemos a correção gama no final do shader), atenuamos as fontes de luz pela fisicamente correta lei do quadrado-inverso .

Então, para cada luz queremos calcular o termo completo Cook-Torrance BRDF:

\[\frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)}\]

A primeira coisa a se fazer é calcular a razão entre as reflexões especular e difusa, ou quanto a superfície reflete luz versus o quanto refrata a luz. Sabemos do capítulo anterior que a equação de Fresnel calcula exatamente isto:

vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
    return F0 + (1.0 - F0) * pow(max(1.0 - cosTheta, 0.0), 5.0);
}  

A aproximação de Fresnel-Schlick espera um parâmetro F0 que é conhecido como a reflexão da superfície na incidência zero ou quanto a superfície reflete se olhar diretamente para a superfície. O F0 varia de acordo com o material e é tingido em metais, conforme encontramos em grandes bancos de dados de materiais. No metallic workflow PBR, fazemos a suposição simplificadora de que a maioria das superfícies dielétricas parecem visualmente corretas com uma constante F0 de 0.04, enquanto especificamos F0 para superfícies metálicas conforme dado pelo valor de albedo. Isso se traduz em código da seguinte maneira:

vec3 F0 = vec3(0.04); 
F0      = mix(F0, albedo, metallic);
vec3 F  = fresnelSchlick(max(dot(H, V), 0.0), F0);

Como você pode ver, para superfícies não-metálicas F0 vale sempre 0.04. Para superfícies metálicas, variamos F0 interpolando linearmente entre o valor original de F0 e o valor de albedo dado pela propriedade metallic .

Dado $F$, os termos restantes são a função de distribuição normal $D$ e a função de geometria $G$.

Em um shader de iluminação direta PBR, seus códigos equivalentes são:

float DistributionGGX(vec3 N, vec3 H, float roughness)
{
    float a      = roughness*roughness;
    float a2     = a*a;
    float NdotH  = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;
	
    float num   = a2;
    float denom = (NdotH2 * (a2 - 1.0) + 1.0);
    denom = PI * denom * denom;
	
    return num / denom;
}

float GeometrySchlickGGX(float NdotV, float roughness)
{
    float r = (roughness + 1.0);
    float k = (r*r) / 8.0;

    float num   = NdotV;
    float denom = NdotV * (1.0 - k) + k;
	
    return num / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2  = GeometrySchlickGGX(NdotV, roughness);
    float ggx1  = GeometrySchlickGGX(NdotL, roughness);
	
    return ggx1 * ggx2;
}

O que é importante notar aqui é que em contraste ao capítulo de teoria, passamos o parâmetro roughness diretamente para essas funções; deste modo podemos fazer algumas modificações específicas para cada termo no valor original de roughness. Baseados em observações pela Disney e adotados pela Epic Games, a iluminação parece mais correta ao elevar ao quadrado o roughness em ambas funções de geometria e distribuição normal.

Com as funções definidas, calcular o NDF e o termo G no loop de refletância é trivial:

float NDF = DistributionGGX(N, H, roughness);       
float G   = GeometrySmith(N, V, L, roughness);       

Isto nos dá informação suficiente para calcular a Cook-Torrance BRDF:

vec3 numerator    = NDF * G * F;
float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0);
vec3 specular     = numerator / max(denominator, 0.001);  

Note que limitamos o denominador para 0.001 para previnir uma divisão por zero no caso de qualquer produto escalar resultar em 0.0.

Agora podemos finalmente calcular cada contribuição de luz a equação de refletância. Como o valor de Fresnel corresponde diretamente a $k_S$, podemos usar F para denotar a contribuição especular de qualquer luz que atinja a superfície. A partir de $k_S$ podemos então calcular a razão de refração $k_D$:

vec3 kS = F;
vec3 kD = vec3(1.0) - kS;
  
kD *= 1.0 - metallic;	

Observando como kS representa a energia da luz que é refletida, a razão restante da energia da luz é a luz que é refratada a qual armazenamos em kD . Além disso, como superfícies metálicas não refratam luz e portanto não têm reflexões difusas, asseguramos esta propriedade ao zerar kD quando a superfície é metálica. Isso nos dá a informação final de que precisamos para calcular o valor de refletância de cada luz de saída.

    const float PI = 3.14159265359;
  
    float NdotL = max(dot(N, L), 0.0);        
    Lo += (kD * albedo / PI + specular) * radiance * NdotL;
}

O valor resultante Lo , ou a radiância de saída, é efetivamente o resultado da integral $\int$ sobre $\Omega$ da equação de refletância. Nós não precisamos resolver a integral para todas as direções de incidência de luz dado que sabemos exatamente as 4 direções incidentes de luz que podem influenciar o fragmento. Por causa disso, podemos iterar diretamente sobre estas direções de luz incidente, ou seja, sobre o número de luzes na cena.

O que resta é adicionar um termo (improvisado) ambiente ao resultado Lo de iluminação direta, e então teremos a cor final da iluminação do fragmento:

vec3 ambient = vec3(0.03) * albedo * ao;
vec3 color   = ambient + Lo;  

Renderização Linear e HDR

Até agora, assumimos que todos os nossos cálculos estão no espaço de cores linear e, para dar conta disso, precisamos corrigir o gama no final do shader. Calcular a iluminação em um espaço linear é extremamente importante, pois o PBR requer que todas as entradas sejam lineares. Não levar isso em consideração resultará em iluminação incorreta. Além disso, queremos que as entradas de luz sejam próximas de seus equivalentes físicos, de modo que seus valores de brilho ou cor possam variar muito em um alto espectro de valores. Como resultado, Lo pode crescer muito rapidamente e então ficar preso entre 0.0 e 1.0 devido à saída padrão de baixa faixa dinâmica ( low dynamic range )(LDR). Corrigimos isso tomando Lo e tom ou mapa de exposição do valor de alta faixa dinâmica ( high dynamic range ) (HDR) corretamente para LDR antes da correção de gama:

color = color / (color + vec3(1.0));
color = pow(color, vec3(1.0/2.2)); 

Aqui aplicamos o mapa de tons na cor HDR usando o operador Reinhard, preservando a alta faixa dinâmica de uma possível irradiância altamente variável, após o qual fazemos a correção gama. Não temos um frambuffer separado ou estádio de pós-processamento, portanto podemos aplicar diretamente ambos tone mapping e correção gama no final do shader de fragmento.

Levar em consideração o espaço de cores linear e a alta faixa dinâmica é extremamente importante em um pipeline de PBR. Sem eles, é impossível capturar corretamente os detalhes altos e baixos de intensidades de luz variáveis e seus cálculos acabam incorretos e, portanto, visualmente desagradáveis.

Shader PBR de Iluminação Direta Completo

Tudo o que resta agora é passar o tom final mapeado e a cor com correção de gama para o canal de saída do shader de fragmento e temos um shader de iluminação PBR direta. Para fins de integridade, a função main completa está listada abaixo:

#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;

// material parameters
uniform vec3  albedo;
uniform float metallic;
uniform float roughness;
uniform float ao;

// lights
uniform vec3 lightPositions[4];
uniform vec3 lightColors[4];

uniform vec3 camPos;

const float PI = 3.14159265359;
  
float DistributionGGX(vec3 N, vec3 H, float roughness);
float GeometrySchlickGGX(float NdotV, float roughness);
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness);
vec3 fresnelSchlick(float cosTheta, vec3 F0);

void main()
{		
    vec3 N = normalize(Normal);
    vec3 V = normalize(camPos - WorldPos);

    vec3 F0 = vec3(0.04); 
    F0 = mix(F0, albedo, metallic);
	           
    // reflectance equation
    vec3 Lo = vec3(0.0);
    for(int i = 0; i < 4; ++i) 
    {
        // calculate per-light radiance
        vec3 L = normalize(lightPositions[i] - WorldPos);
        vec3 H = normalize(V + L);
        float distance    = length(lightPositions[i] - WorldPos);
        float attenuation = 1.0 / (distance * distance);
        vec3 radiance     = lightColors[i] * attenuation;        
        
        // cook-torrance brdf
        float NDF = DistributionGGX(N, H, roughness);        
        float G   = GeometrySmith(N, V, L, roughness);      
        vec3 F    = fresnelSchlick(max(dot(H, V), 0.0), F0);       
        
        vec3 kS = F;
        vec3 kD = vec3(1.0) - kS;
        kD *= 1.0 - metallic;	  
        
        vec3 numerator    = NDF * G * F;
        float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0);
        vec3 specular     = numerator / max(denominator, 0.001);  
            
        // add to outgoing radiance Lo
        float NdotL = max(dot(N, L), 0.0);                
        Lo += (kD * albedo / PI + specular) * radiance * NdotL; 
    }   
  
    vec3 ambient = vec3(0.03) * albedo * ao;
    vec3 color = ambient + Lo;
	
    color = color / (color + vec3(1.0));
    color = pow(color, vec3(1.0/2.2));  
   
    FragColor = vec4(color, 1.0);
}  

Felizmente, com a teoria do capítulo anterior e o conhecimento da equação de refletância, esse shader não deve ser mais tão assustador. Se pegarmos este shader, 4 luzes pontuais e algumas esferas onde variamos seus valores metálicos e de rugosidade em seus eixos vertical e horizontal, respectivamente, obteríamos algo assim:

De baixo para cima, o valor metálico varia de 0.0 a 1.0, com a rugosidade aumentando da esquerda para a direita de 0.0 a 1.0. Você pode ver que apenas alterando esses dois parâmetros simples de entender, já podemos exibir uma grande variedade de materiais diferentes.

Você pode encontrar o código-fonte completo da demonstração aqui

PBR Texturizado

Estender o sistema para aceitar seus parâmetros de superficies como texturas ao invés de valores uniformes nos dá um controle por fragmento sobre as propriedades do material da superfície:

[...]
uniform sampler2D albedoMap;
uniform sampler2D normalMap;
uniform sampler2D metallicMap;
uniform sampler2D roughnessMap;
uniform sampler2D aoMap;
  
void main()
{
    vec3 albedo     = pow(texture(albedoMap, TexCoords).rgb, 2.2);
    vec3 normal     = getNormalFromNormalMap();
    float metallic  = texture(metallicMap, TexCoords).r;
    float roughness = texture(roughnessMap, TexCoords).r;
    float ao        = texture(aoMap, TexCoords).r;
    [...]
}

Observe que as texturas de albedo que vêm de artistas são geralmente criadas no espaço sRGB, e é por isso que primeiro as convertemos em espaço linear antes de usar albedo em nossos cálculos de iluminação. Com base no sistema que os artistas usam para gerar mapas de oclusão de ambiente, você também pode ter que convertê-los de sRGB para espaço linear. Mapas metálicos e de rugosidade são quase sempre criados no espaço linear.

Substituir as propriedades do material do conjunto anterior de esferas por texturas já mostra uma grande melhoria visual em relação aos algoritmos de iluminação anteriores que usamos:

Você pode encontrar o código-fonte completo da demonstração texturizada aqui e o conjunto de texturas usado aqui (com um mapa ao branco). Lembre-se de que as superfícies metálicas tendem a parecer muito escuras em ambientes com iluminação direta, pois não têm refletância difusa. Eles parecem mais corretos quando se leva em consideração a iluminação especular do ambiente, que é o que vamos nos concentrar nos próximos capítulos.

Embora não seja tão visualmente impressionante quanto algumas das demos de renderização PBR que você encontra por aí, dado que ainda não temos iluminação baseada em imagem, o sistema que temos agora ainda é um renderizador baseado fisicamente e mesmo sem IBL podemos ver sua iluminação parecer muito mais realista.