Iluminação Básica

Post Original

Iluminação no mundo real é extremamente complicada e depende de muitos fatores, algo que não podemos dar ao luxo de calcular com o poder de processamento limitado que temos. Iluminação em OpenGL é, portanto, feita com base em aproximações da realidade, utilizando modelos simplificados que são muito mais fáceis de se processar e se parece relativamente similar. Estes modelos de iluminação são baseados na física da luz como a entendemos. Um desses modelos é chamado o modelo de iluminação Phong . O modelo de iluminação Phong é composto de 3 componentes: iluminações ambiente, difusa e especular. Abaixo você pode ver o que esses componentes de iluminação fazem sozinhos e combinados:

• Iluminação Ambiente : mesmo quando está escuro, geralmente ainda há alguma luz em algum lugar no mundo (a lua, uma luz distante), então os objetos quase nunca estão completamente no escuro. Para simular isso, usamos uma constante de iluminação ambiente que sempre dá ao objeto um pouco de cor.

• Iluminação Difusa : simula o impacto direcional que um objeto luz tem sobre um objeto. Este é a componente mais visualmente significativa do modelo de iluminação. Quanto mais uma parte de um objeto se alinha a fonte de luz, mais clara se torna.

• Iluminação Especular : simula o ponto brilhante de uma luz que aparece em objetos brilhantes. Highlights especulares são mais inclinados à cor da luz do que a cor do objeto.

Para criar cenas visualmente interessantes queremos, pelo menos, simular estas 3 componentes de iluminação. Vamos começar com a mais simples: iluminação ambiente.

Iluminação Ambiente (Ambient lighting)

A luz geralmente não vem de uma única fonte, mas a partir de muitas fontes de luz espalhadas ao redor de nós, mesmo quando elas não são imediatamente visíveis. Uma das propriedades da luz é que ela pode se espalhar e rebater em muitas direções, atingindo pontos que não são diretamente visíveis; a luz pode, assim, refletir sobre outras superfícies e ter um impacto indireto sobre a iluminação de um objeto. Algoritmos que levam isso em consideração são chamados algoritmos de iluminação global ( global illumination , mas estes são complicados e caros para calcular.

Uma vez que não somos grandes fãs de algoritmos complicados e caros, vamos começar usando um modelo muito simplista de iluminação global, ou seja, iluminação ambiente . Como você viu na seção anterior, usamos uma pequena cor (de luz) constante que podemos adicionar à cor final resultante dos fragmentos do objeto, fazendo parecer que há sempre alguma luz difusa, mesmo quando não há uma fonte de luz direta.

Adicionando iluminação ambiente a cena é realmente fácil. Pegamos a cor da luz, a multiplicamos por um pequeno fator constante de ambiente, multiplicamos então com a cor do objeto, e que o usamos o resultado como cor do fragmento no shader do cubo:

void main()
{
    float ambientStrength = 0.1;
    vec3 ambient = ambientStrength * lightColor;

    vec3 result = ambient * objectColor;
    FragColor = vec4(result, 1.0);
}  

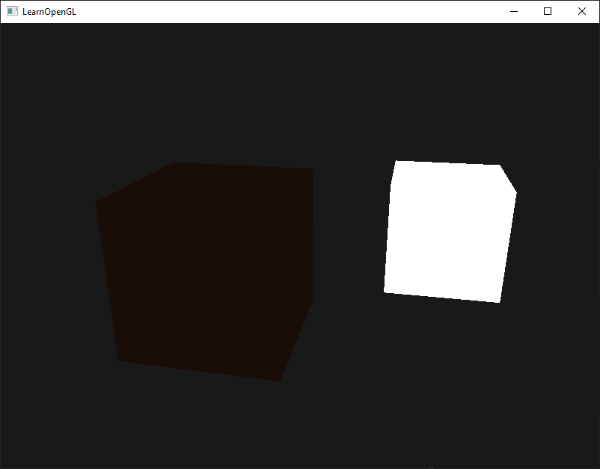
Se você executar o programa agora, vai perceber que a primeira fase de iluminação é agora aplicada ao objeto com sucesso. O objeto está bastante escuro, mas não totalmente, uma vez que a iluminação ambiente é aplicada (note que o cubo de luz não é afetado porque usamos um shader diferente). O resultado então é algo assim:

Iluminação Difusa (Diffuse lighting)

A iluminação ambiente por si só não produz os resultados mais interessantes, mas a iluminação difusa no entanto vai começar a dar um impacto visual significativo sobre o objeto. A Iluminação difusa dá ao objeto mais brilho quanto mais perto os seus fragmentos estão alinhados com os raios de luz a partir de uma fonte de luz. Para lhe dar uma melhor compreensão dê uma olhada a seguinte imagem:

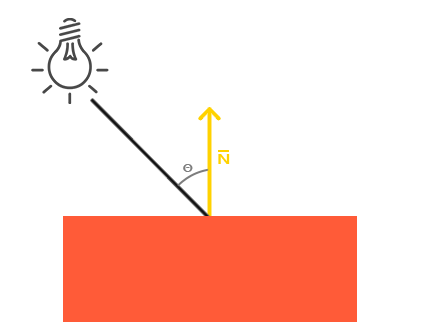
Na esquerda, encontramos uma fonte de luz com um raio de luz dirigido a um único fragmento de nosso objeto. Precisamos medir em que ângulo o raio de luz atinge o fragmento. Se o raio de luz é perpendicular à superfície do objeto a luz tem o maior impacto. Para medir o ângulo entre o raio de luz e o fragmento usamos algo chamado um de vetor normal ( normal vector ), que é um vetor perpendicular à superfície do fragmento (aqui representada como uma seta amarela); nós vamos falar disso mais tarde. O ângulo entre os dois vetores pode então ser facilmente calculado com o produto escalar.

Você pode se lembrar do capítulo de transformações que, quanto menor o ângulo entre dois vetores unitários, mais o produto escalar é inclinado para um valor de 1. Quando o ângulo entre os dois vetores é de 90 graus, o produto escalar se torna 0. O mesmo se aplica a $\theta$: quanto maior $\theta$ é, menos impacto a luz deve ter na cor do fragmento.

O produto escalar resultante é, portanto, um escalar que podemos utilizar para calcular o impacto da luz sobre a cor do fragmento, resultando em fragmentos de diferente brilhos com base na sua orientação para a luz.

Então, o que precisamos para calcular a iluminação difusa é:

• Vetor normal: um vetor que é perpendicular à superfície do vértice.

• O raio de luz direcionado: um vetor de direção que é o vetor de diferença entre a posição da luz e a posição do fragmento. Para calcular este raio de luz, precisamos do vetor posição da luz e vetor posição do fragmento.

Vetores Normais (Normal Vectors)

Um vetor normal é um vetor (unitário) que é perpendicular à superfície de um vértice. Como um vértice, por si só, não tem superfície (é apenas um único ponto no espaço) temos que extrair um vetor normal usando seus vértices vizinhos e descobrir a superfície do vértice. Podemos usar um pequeno truque para calcular os vetores normais para todos os vértices do cubo usando o produto vetorial ( cross product ), mas já que um cubo 3D não é uma forma complicada podemos simplesmente adicioná-los manualmente para os dados de vértice. o array de dados de vértice atualizado pode ser encontrado [aqui]((/code_viewer.php?code=lighting/basic_lighting_vertex_data). Tente perceber que as normais são na verdade vetores perpendiculares à superfície de cada plano (um cubo consiste em 6 planos).

Como adicionamos dados extra ao array de vértice devemos atualizar shader de vértice do cubo:

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
...

Agora que nós adicionamos um vetor normal a cada um dos vértices e atualizamos o shader de vértice devemos atualizar os ponteiros de atributos vértice também. Note que o cubo de luz usa o mesmo array de vértices para seus dados de vértice, mas o shader da lâmpada não usa nenhum dos vetores normais recém-adicionados. Não temos que atualizar os shaders da lâmpada ou configurações de atributos, mas temos que, pelo menos, modificar os ponteiros de atributos de vértice para refletir o tamanho do novo array de vértice:

glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)0);
glEnableVertexAttribArray(0);

Nós só queremos usar os primeiros 3 floats de cada vértice e ignorar os últimos 3 floats por isso só precisamos atualizar o parâmetro de stride para 6 vezes o tamanho de um float.

Todos os cálculos de iluminação são feitos no shader de fragmento e por isso precisamos transmitir os vetores normais do shader vértice para o shader de fragmento. Vamos fazer isso:

out vec3 Normal;

void main()
{
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    Normal = aNormal;
} 

O que resta fazer agora é declarar a variável de entrada correspondente no shader de fragmento:

in vec3 Normal;  

Calculando a Cor Difusa

Agora temos o vetor normal para cada vértice, mas ainda precisamos do vetor posição da luz e o vetor posição do fragmento. Como a posição da luz é uma única variável estática podemos declará-lo como um uniforme no shader de fragmento:

uniform vec3 lightPos;  

E, em seguida, atualizar o uniforme no loop de renderização (ou fora, uma vez que não muda a todo quadro ( frame ). Usamos o vetor lightPos declarado no capítulo anterior como a localização da fonte de luz difusa:

lightingShader.setVec3("lightPos", lightPos);  

Então a última coisa que precisamos é a verdadeira posição do fragmento. Nós vamos fazer todos os cálculos de iluminação no espaço de mundo, por isso queremos primeiramente uma posição de vértice que também está no espaço de mundo. Podemos fazer isso através da multiplicação do atributo de posição vértice com apenas a matriz de modelo (não a matriz de visão nem a matriz de projeção) para transformá-lo em coordenadas espaciais de mundo. Isto pode ser facilmente realizado no shader de vértice, então vamos declarar uma variável de saída e calcular suas coordenadas espaciais de mundo:

out vec3 FragPos;  
out vec3 Normal;
  
void main()
{
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    FragPos = vec3(model * vec4(aPos, 1.0));
    Normal = aNormal;
}

E, por último adicione a variável de entrada correspondente ao shader de fragmento:

in vec3 FragPos;  

Esta variável in irá ser interpolada a partir dos 3 vetores de posição de mundo do triângulo para formar o vetor FragPos , que é a posição de mundo por fragmento. Agora que todas as variáveis ​​necessárias estão definidas podemos começar os cálculos de iluminação.

A primeira coisa que precisamos calcular é o vetor de direção entre a fonte luminosa e a posição do fragmento. Da seção anterior, sabemos que o vetor direção da luz é o vetor diferença entre o vetor posição da luz e vetor posição do fragmento. Como você pode se lembrar do capítulo de transformações podemos facilmente calcular essa diferença subtraindo os dois vetores um do outro. Nós também queremos garantir que todos os vetores relevantes acabem como vetores unitários, então normalizamos tanto a normal e o vetor direção resultantes:

vec3 norm = normalize(Normal);
vec3 lightDir = normalize(lightPos - FragPos);  

Em seguida, precisamos calcular o impacto da luz difusa sobre o fragmento atual, tomando o produto escalar entre os vetores norma e lightDir . O valor resultante é então multiplicado com a cor da luz para se obter a componente difusa, resultando em uma componente difusa mais escura quanto maior o ângulo entre os dois vetores:

float diff = max(dot(norm, lightDir), 0.0);
vec3 diffuse = diff * lightColor;

Se o ângulo entre os dois vetores é superior a 90 graus, então o resultado do produto escalar será negativo e vamos acabar com uma componente difusa negativa. Por essa razão, usamos a função max que retorna o maior de seus parâmetros para garantir que a componente difusa (e, portanto, as cores) nunca se torne negativa. A iluminação para cores negativas não é definida de fato, por isso é melhor ficar longe dela, a menos que você seja um daqueles artistas excêntricos.

Agora que temos tanto uma componente ambiente e uma componente difusa, somamos as duas cores e, em seguida, multiplicamos o resultado com a cor do objeto para obter a cor de saída do fragmento:

vec3 result = (ambient + diffuse) * objectColor;
FragColor = vec4(result, 1.0);

Se o sua aplicação (e shaders) compilaram com sucesso você deve ver algo assim:

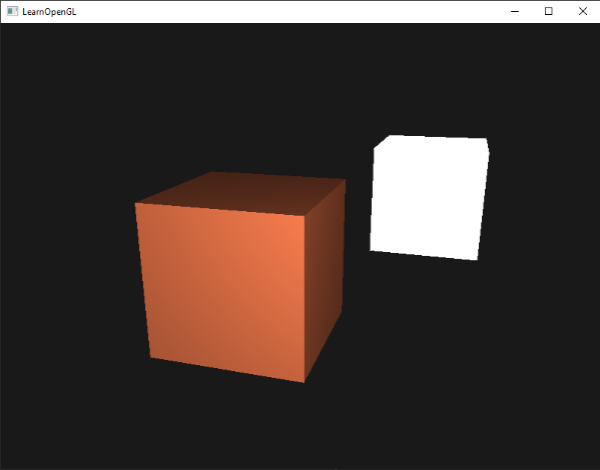
Você pode ver que com a iluminação difusa o cubo começa a parecer um cubo real novamente. Tente visualizar os vetores normais em sua cabeça e mover a câmera ao redor do cubo para ver que quanto maior o ângulo entre o vetor normal e vetor de direção da luz, mais escuro fica o fragmento.

Se estiver travado, sinta-se livre para comparar o seu código-fonte com o código-fonte completo aqui.

Uma Última Coisa

Na seção anterior, passamos o vetor normal diretamente do shader de vértice ao shader de fragmento. No entanto, os cálculos no shader de fragmento são todos feitos no espaço de mundo, por isso não deveríamos transformar os vetores normais a coordenadas espaciais de mundo também? Basicamente sim, mas não é tão simples como simplesmente multiplicá-los com a matriz de modelo.

Primeiro de tudo, vetores normais são apenas vetores de direção e não representam uma posição específica no espaço. Em segundo lugar, os vetores normais não têm uma coordenada homogênea (a componente w de uma posição de vértice). Isto significa que translações não deveriam ter nenhum efeito sobre os vetores normais. Portanto, se queremos multiplicar os vetores normais com uma matriz de modelo, devemos remover a parte de translação da matriz pegando a matriz 3x3 superior esquerde da matriz de modelo (note que nós também poderíamos definir o componente w de um vetor normal para 0 e multiplicar com a matriz de 4x4).

Em segundo lugar, se a matriz de modelo realizasse uma escala não-uniforme, os vértices seriam alterados de tal maneira que o vetor normal não mais seria perpendicular à superfície. A figura seguinte mostra o efeito que uma matriz de modelo (com a escala não uniforme) tem sobre um vetor normal:

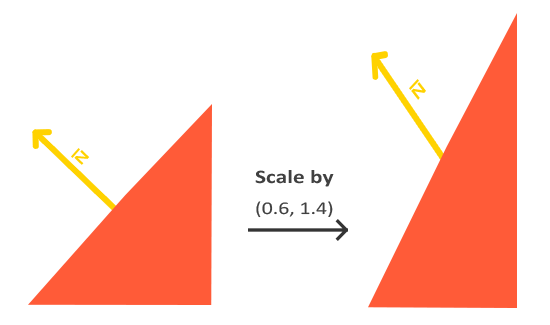
Sempre que aplicamos uma escala não-uniforme (nota: uma escala uniforme só muda magnitude da normal, não a sua direção, o que é facilmente corrigida com sua normalização) os vetores normais não são mais perpendiculares à superfície correspondente, o que distorce a iluminação.

O truque para corrigir este comportamento é a utilização de uma matriz de modelo diferente especificamente adaptada para vetores normais. Esta matriz é chamada de matriz normal ( normal matrix ) e usa algumas operações algébricas lineares para remover o efeito de escalar de forma errada os vetores normais. Se você quiser saber como essa matriz é calculada sugiro o seguinte artigo.

A matriz normal é definida como "a transposta da inversa da parte 3x3 superior esquerda da matriz de modelo". Ufa, é um bocado de palavra aí e se você realmente não entender o que isso significa, não se preocupe; não discutimos inversas e matrizes de transposição ainda. Note que a maioria dos recursos definem a matriz normal como calculada a partir da matriz de modelo-visão, mas uma vez que estamos trabalhando no espaço de mundo (e não no espaço de visão), vamos derivá-la a partir da matriz de modelo.

No shader de vértice podemos gerar a matriz normal, utilizando as funções inverse e transpose no shader de vértice que funcionam em qualquer tipo de matriz. Note que damos um cast na matriz para uma matriz 3x3 para garantir que ela perca suas propriedades de translação e para que possamos multiplicá-la com o vetor normal vec3:

Normal = mat3(transpose(inverse(model))) * aNormal;  

Na seção de iluminação difusa a iluminação ficou boa porque nós não fizemos nenhuma escala no objeto, de modo que não era realmente necessário usar uma matriz normal e nós poderíamos ter apenas multiplicado as normais com a matriz de modelo. No entanto, se você estiver fazendo uma escala não uniforme, é essencial que você multiplique seus vetores normais com a matriz normal.

Iluminação Especular (Specular Lighting)

Se você não já estiver esgotado(a) com toda essa conversa de iluminação podemos terminar o modelo de iluminação Phong adicionando reflexos especulares.

Semelhante a iluminação difusa, a iluminação especular é baseada no vetor de direção da luz e os vetores normais do objeto, mas, desta vez, também na direção da visão, isto é, na direção em que o jogador está olhando para o fragmento. A iluminação especular baseia-se nas propriedades de reflexão das superfícies. Se pensarmos na superfície do objeto como um espelho, a iluminação especular é mais forte onde víssemos a luz refletida na superfície. Você pode ver este efeito na imagem a seguir:

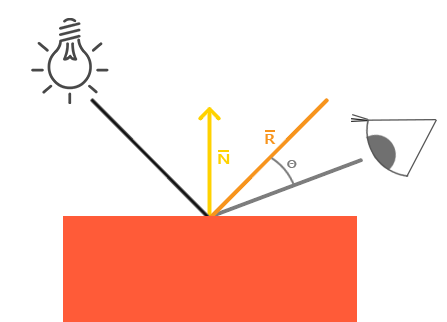
Calculamos um vetor de reflexão, refletindo a direção da luz em torno do vetor normal. Em seguida, calculamos a distância angular entre este vector de reflexão e a direção da visão. Quanto mais próximo o ângulo entre eles, maior o impacto da luz especular. O efeito resultante é que vemos um pouco de highlight quando nós estamos olhando para a direção da luz refletida através da superfície.

O vetor de visão (da câmera) é a variável extra que precisamos para a iluminação especular, a qual podemos calcular usando a posição no espaço de mundo do espectador e a posição do fragmento. Em seguida, calculamos a intensidade da especular, multiplicamos esta intensidade com a cor da luz e adicionamos as componentes de ambiente e difusa.

Para obter as coordenadas espaciais de mundo do espectador nós simplesmente tomamos o vetor posição da câmera (que é o espectador é claro). Então, vamos adicionar outro uniforme para o shader de fragmento e passar o vetor posição da câmera para o shader:

uniform vec3 viewPos;

lightingShader.setVec3("viewPos", camera.Position); 

Agora que temos todas as variáveis ​​necessárias podemos calcular a intensidade especular. Primeiro vamos definir um valor de intensidade especular para dar uma cor meio brilhante ao brilho especular para que ele não tenha muito impacto:

float specularStrength = 0.5;

Se escolhêssemos o valor de 1.0f teríamos uma componente especular muito brilhante que é um pouco demais para um cubo coral. No próximo capítulo vamos falar sobre como definir corretamente todas essas intensidades de iluminação e como elas afetam os objetos. Em seguida calculamos o vetor direção da câmera e o vetor correspondente de reflexão ao longo do eixo normal:

vec3 viewDir = normalize(viewPos - FragPos);
vec3 reflectDir = reflect(-lightDir, norm);  

Note que negamos o vetor lightDir. A função reflect espera que o primeiro vetor apontar da fonte de luz para a posição do fragmento, mas o vetor lightDir está apontando na direção contrária: a partir do fragmento para a fonte de luz (isto depende da ordem de subtração anterior quando calculamos o vetor lightDir). Para ter certeza de que obteremos o vetor reflect correto, invertemos a sua direção, negando o vetor lightDir primeiro. O segundo argumento espera um vetor normal, então fornecemos o vetor normal normalizado.

Então o que resta a fazer é realmente calcular a componente especular. Isto é feito com a seguinte fórmula:

float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);
vec3 specular = specularStrength * spec * lightColor;  

Calculamos primeiro o produto escalar entre a direção da câmera e a direção de reflexão (e certifique-se que este vetor não é negativo) e, em seguida, elevamos o resultado a potência de 32. Este valor de 32 é o valor de brilhosidade ( shininess do highlight. Quanto maior o valor de brilhosidade de um objeto, mais ele reflete adequadamente a luz em vez de espalhá-la ao seu redor e, portanto, menor o highlight se torna. Abaixo você pode ver uma imagem que mostra o impacto visual de diferentes valores de brilhosidade:

Nós não queremos que a componente especular chame muito a atenção, então mantemos o expoente de 32. A única coisa que resta a fazer é adicioná-la as componentes de ambiente e difusa e multiplicar o resultado combinando com a cor do objeto:

vec3 result = (ambient + diffuse + specular) * objectColor;
FragColor = vec4(result, 1.0);

Nós agora calculamos todos as componentes de iluminação do modelo de iluminação Phong. Com base no seu ponto de vista você deve ver algo como isto:

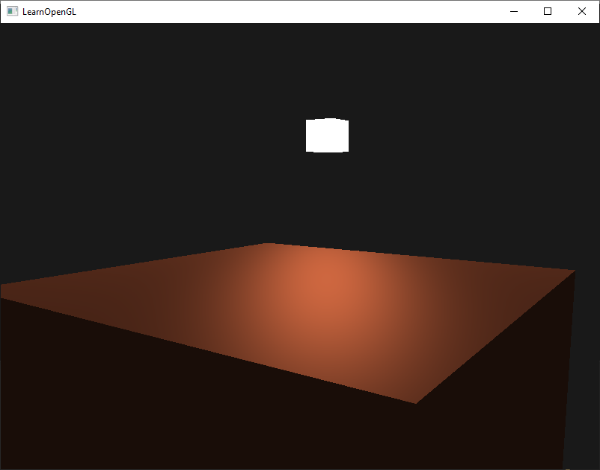
Você pode encontrar o código-fonte completo aqui.

Nos primórdios dos shaders de iluminação, os desenvolvedores implementavam o modelo de iluminação Phong no shader de vértice. A vantagem de fazer iluminação no shader de vértice é que é muito mais eficiente, uma vez que geralmente existem muito menos vértices do que fragmentos, de modo que os cálculos de iluminação são feitos com menos frequência. No entanto, o valor da cor resultante no shader de vértice é o da iluminação de cor resultante somente no vértice e os valores de cor dos fragmentos vizinhos são, em seguida, o resultado de cores de iluminação interpolados. O resultado era que a iluminação não era muito realista, a menos que fossem utilizadas grandes quantidades de vértices:

Quando o modelo de iluminação Phong é implementado no shader de vértice ele é chamado shading de Gouraud ( Gouraud shading ) em vez de Phong shading . Note-se que devido à interpolação a iluminação parece um pouco fora do lugar. O Phong shading dá resultados iluminação muito mais suaves.

A partir de agora você deve estar começando a ver quão poderosos são os shaders. Com pouca informação, shaders são capazes de calcular como a iluminação afeta as cores de fragmento para todos os nossos objetos. Nos próximos capítulos vamos nos aprofundar muito mais no que podemos fazer com o modelo de iluminação.

Exercícios

• A nossa fonte de luz é uma fonte de luz estática muito chata. Tente mover a fonte de luz ao redor da cena ao longo do tempo usando um sin ou cos . Observando a mudança de iluminação ao longo do tempo lhe dará uma boa compreensão do modelo de iluminação de Phong: solução.

• Brinque com diferentes valores para as componentes de ambiente, difusa e especular e veja como impactam o resultado. Também experimente com o fator de brilhosidade. Tente compreender por que certos valores têm uma certa saída visual.

• Faça shading de Phong no espaço de visão em vez do espaço de mundo: solução.

• Implemente o shading de Gouraud em vez do shading de Phong. Se você fez as coisas direito a iluminação deve parecer um pouco fora do lugar (especialmente os reflexos especulares) com o objeto do cubo. Tente pensar por que parece tão estranho: solução